题目内容
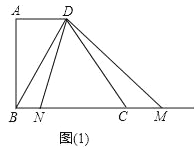
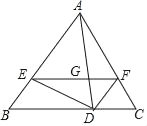
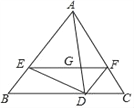
【题目】如图在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且∠ADE=∠B,∠ADF=∠C,线段EF交线段AD于点G.
(1)求证:AE=AF;
(2)若![]() ,求证:四边形EBDF是平行四边形.
,求证:四边形EBDF是平行四边形.
【答案】见解析
【解析】试题分析:
(1)由已知条件易证△BAD∽△DAE,由此可得![]() ,则AD2=AEAB;同理可得AD2=AFAC,从而可得AEAB=AFAC,结合AB=AC即可得到AE=AF;
,则AD2=AEAB;同理可得AD2=AFAC,从而可得AEAB=AFAC,结合AB=AC即可得到AE=AF;
(2)由(1)可得∠AED=∠ADB=∠DAC+∠C,结合∠DFC=∠DAC+∠ADF,∠ADF=∠C,可得∠AED=∠DFC,这样结合![]() ,可得△AED∽△CFD,由此可得∠ADE=∠CDF=∠B,则DF∥BE;由AE=AF,AB=AC可得∠AEF=∠AFE,∠B=∠C,结合2∠AEF+∠BAC=180°,2∠B+∠BAC=180°,可得∠AEF=∠B,从而可得EF∥BC;这样即可得到所求结论了.
,可得△AED∽△CFD,由此可得∠ADE=∠CDF=∠B,则DF∥BE;由AE=AF,AB=AC可得∠AEF=∠AFE,∠B=∠C,结合2∠AEF+∠BAC=180°,2∠B+∠BAC=180°,可得∠AEF=∠B,从而可得EF∥BC;这样即可得到所求结论了.
试题解析:
(1)∵∠ADE=∠B,∠BAD=∠EAD,
∴△BAD∽△DAE,
∴![]() ,
,
∴AD2=AEAB,
同法可证:AD2=AFAC,
∴AEAB=AFAC,∵AB=AC,
∴AE=AF;
(2)∵△BAD∽△DAE,
∴∠AED=∠ADB=∠DAC+∠C,
∵∠DFC=∠DAC+∠ADF,∠ADF=∠C,
∴∠AED=∠DFC,
∵![]() ,
,
∴△AED∽△CFD,
∴∠ADE=∠CDF=∠B,
∴DF∥BE,
∵AE=AF,AB=AC,
∴∠AEF=∠AFE,∠B=∠C,
∵2∠AEF+∠BAC=180°,2∠B+∠BAC=180°,
∴∠AEF=∠B,
∴EF∥BC,
∴四边形EBDF是平行四边形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目