题目内容
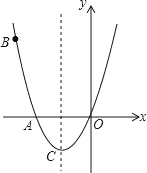
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足是M,是否存在点p,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x(2)(1,3)(3)(![]() ,
,![]() )或(3,15)
)或(3,15)
【解析】试题分析:(1)由于抛物线经过A(﹣2,0),B(﹣3,3)及原点O,待定系数法即可求出抛物线的解析式。
(2)根据平行四边形的性质,对边平行且相等,可以求出点D的坐标。
(3)分两种情况讨论,①△AMP∽△BOC,②PMA∽△BOC,根据相似三角形对应边的比相等可以求出点P的坐标。

练习册系列答案
相关题目