��Ŀ����
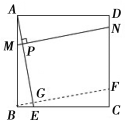
����Ŀ���ס��������ֱ��![]() ����������У��׳���
����������У��׳���![]() �س���
�س���![]() ���ҳ���
���ҳ���![]() �س��������׳�����
�س��������׳�����![]() �غ�ֱ�Ӱ�ԭ·ԭ�ٷ��أ����ҳ�����
�غ�ֱ�Ӱ�ԭ·ԭ�ٷ��أ����ҳ�����![]() �غ�����Ϣ
�غ�����Ϣ![]() �ٰ�ԭ·ԭ�ٷ��أ���ͼ�Ǽס���������
�ٰ�ԭ·ԭ�ٷ��أ���ͼ�Ǽס���������![]() �ؾ���
�ؾ���![]() ����λ��
�����![]() ����
����![]() �����
����λ��![]() ����׳�����ʻʱ��
����׳�����ʻʱ��![]() ����λ��
����λ��![]() ��֮��ĺ���ͼ��
��֮��ĺ���ͼ��
��1���׳����ٶ��� ![]() ���ҳ����ٶ���
���ҳ����ٶ��� ![]() ����
����![]() ��������
��������
��2�����߶�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���ס�����������ʻ�Ĺ����������˼��Σ�ֱ��д�����ס�����������ʱ�׳���ʻ��ʱ�䣬��������������һ������ʱ����ʱ������![]() �صľ���
�صľ���
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2�� ![]() ����3��2��������
����3��2��������![]() ��
��![]()
��������
��1������ͼ����㼴�ɣ�
��2���ô���ϵ�������㼴�ɣ�
��3�����ͼ����ʽ���㼴�ɣ�
��1����ͼ���֪���׳����ٶȣ�![]() =
=![]() ��km/h����
��km/h����
�ҳ����ٶȣ�![]() =
=![]() ��km/h����
��km/h����
�ҳ�����![]() �غ�����Ϣ
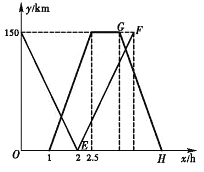
�غ�����Ϣ![]() �ٰ�ԭ·ԭ�ٷ��ؿ�֪�ҳ�����ʱ����ʱ����ȥʱ����ʱ����ͬ���ʵ�H�ĺ�����Ϊ��2.5+1+��2.5-1��=5��
�ٰ�ԭ·ԭ�ٷ��ؿ�֪�ҳ�����ʱ����ʱ����ȥʱ����ʱ����ͬ���ʵ�H�ĺ�����Ϊ��2.5+1+��2.5-1��=5��
�ʵ�H������Ϊ![]() ��
��
��2�������⣬��![]() ��
��![]() ��E��2��0����H��5��0����
��E��2��0����H��5��0����
���߶�![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
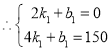 ��
��
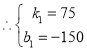 ��
��
![]() ��
��
���߶�![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
ͬ������![]() ��
��![]() ����
����![]() ��
�У�
��![]() ��
��
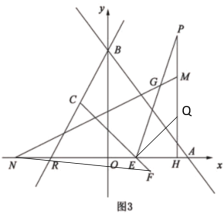
��3����ͼ���֪���ס�����������ʻ;��������![]() �Σ�
�Σ�

���߶�ME��CD�ĺ�����ϵʽ�ֱ�Ϊy=cx+d��y=ex+f��
��������ֱ��з������![]() ��
��![]() ��
��
��������������ֱ��![]() ��
��![]() ��
��
���߶�ME��CD�ĺ�����ϵʽ�ֱ�Ϊy=-75x+150(0��x��2)��y=100x-100(1��x<2.5)��
�ⷽ����![]() ����
����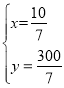 ��
��
�����߶�![]() ��
��![]() �ĺ�����ϵʽ�ⷽ����
�ĺ�����ϵʽ�ⷽ����![]() ����
����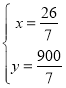 ��
��
![]()
��ס�����������ʱ�׳���ʻ��ʱ��ֱ�Ϊ![]() h��
h��![]() h���������һ������ʱ��������
h���������һ������ʱ��������![]() ��
��![]() ��
��

 ��������ϵ�д�
��������ϵ�д�����Ŀ��ij��ѧ��ȤС��Ϊ�˽�ȫУѧ�����������������ڼ�ʹ���ֻ����������ȤС�������ȡ������ѧ��������������ĩ�����ʹ���ֻ�ʱ�䣬�����ݵ���������������������������ͳ�Ʊ���ͳ��ͼ������ͼ����Ϣ������������⣺
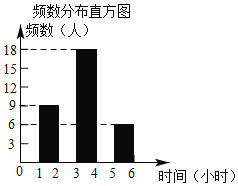
�Ķ�ʱ�� ��Сʱ�� | Ƶ�� ���ˣ� | Ƶ�� |
1��x��2 | 9 | 0.15 |
2��x��3 | a | m |
3��x��4 | 18 | 0.3 |
4��x��5 | 12 | n |
5��x��6 | 6 | 0.1 |
�ϼ� | b | 1 |
��1����գ�a���� ����b���� ����m���� ����n���� ����
��2����Ƶ���ֲ�ֱ��ͼ����������
��3�������ѧ��ѧ������1200�ˣ�����������Ϣ������ȫУѧ������ĩ����ʹ���ֻ�ʱ�䲻����4Сʱ��ѧ����Լ�ж����ˣ�