题目内容
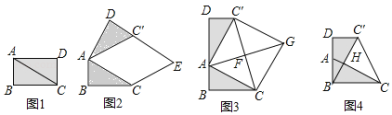
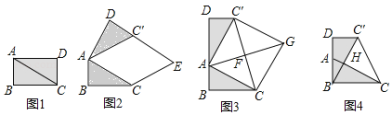
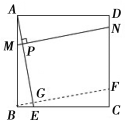
【题目】如图,在正方形ABCD中,E为边BC上一点(不与点B,C重合),垂直于AE的一条直线MN分别交AB,AE,CD于点M,P,N.小聪过点B作BF∥MN分别交AE,CD于点G,F后,猜想线段EC,DN,MB之间的数量关系为EC=DN+MB.他的猜想正确吗?请说明理由.
【答案】正确,理由见解析
【解析】
先证明四边形MBFN是平等四边形,从而得到MB=NF;根据ASA证明△ABE≌△BCF,从而得到BE=CF,则有DF=EC,再根据DF=NF+DN和MB=NF可得到EC=DN+MB.
∵四边形ABCD是正方形,
∴MB//NF,∠C=∠ABC,AB//DC,∠BFC+∠CBF=90,AB=BC,
又∵MN//BF,
∴四边形MBFN是平行四边形,∠AMP=∠ABF,
∴MB=NF,
∵AB//DC,
∴∠BFC=∠ABF,
又∵∠AMP=∠ABF,
∴∠AMP=∠BFC,
∵MN⊥AE,
∴∠APM是直角,则∠AMP+∠MAE=90,
又∵∠BFC+∠CBF=90,
∴∠MAE=CBF,
在△ABE和△BCF中
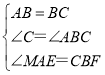 ,
,
∴△ABE≌△BCF(AAS),
∴BE=CF,
∴CE=DF
又∵DF=NF+DN(由图可得),MB=NF(已证)
∴CE=DF=DN+MB,即CE=DN+MB.

练习册系列答案
相关题目