题目内容
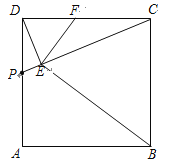
【题目】如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．
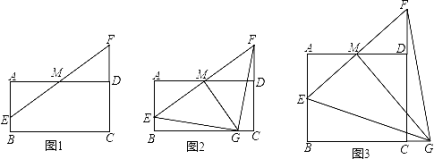
（1）如图1，求证：AE=DF；
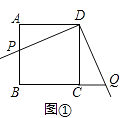
（2）如图2，若AB=2，过点M作 MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形
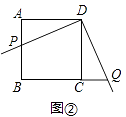
（3）如图3，若AB=
，过点M作 MG⊥EF交线段BC的延长线于点G．
①直接写出线段AE长度的取值范围；
②判断△GEF的形状，并说明理由．
【答案】（1）由△AEM≌△DFM可证得（2）关键是证GE=GF，再证有个角是直角。
（3）①
＜AE≤
． ②△GEF是等边三角形
【解析】
试题分析：解：（1）证明：如图1,在矩形ABCD中，∠EAM=∠FDM=90°，∠AME=∠FMD．
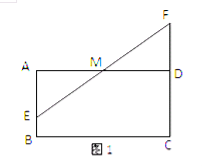
∵M是AD的中点，∴AM=DM，
∴△AEM≌△DFM（ASA）．
∴AE=DF． 2分
（2）证明：如图2，过点G作GH⊥AD于H，
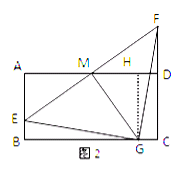
∴∠A=∠B=∠AHG=90°，
∴四边ABGH为矩形，
∴∠AME+∠AEM=90°，
∵MG⊥EF，
∴∠GME=90°．
∴∠AME+∠GMH=90°
∴∠AEM=∠GMH．
∵AD=4，M是AD的中点
∴AM=2
∵四边ABGH为矩形，
∴AB=HG=2
∴AM=HG
∴△AEM≌△HMG（AAS）．
∴ME=MG．
∴∠EGM=45°．
由（1）得△AEM≌△DFM，
∴ME=MF．
∵MG⊥EF，
∴GE=GF．
∴∠EGF=2∠EGM=90°．
∴△GEF是等腰直角三角形． 5分
（3 ）①当C、G重合时，如图4，
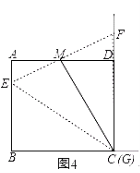
∵四边形ABCD是矩形，
∴∠A=∠ADC=90°，
∴∠AME+∠AEM=90°．
∵MG⊥EF，
∴∠EMG=90°．
∴∠AME+∠DMC=90°，
∴∠AEM=∠DMC，
∴△AEM∽△DMC
∴
，
∴
，
∴AE=
当E、B重合时，AE最长为
，
∴＜AE≤． 7分（注：此小问只需直接写出结果即可）
②如图3，△GEF是等边三角形．
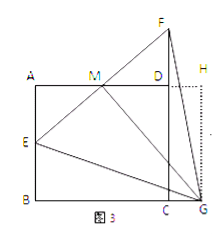
证明：过点G作GH⊥AD交AD延长线于点H，
∵∠A=∠B=∠AHG=90°，
∴四边形ABGH是矩形．
∴GH=AB=2
．
∵MG⊥EF，
∴∠GME=90°．
∴∠AME+∠GMH=90°．
∵∠AME+∠AEM=90°，
∴∠AEM=∠GMH．
又∵∠A=∠GHM=90°，
∴△AEM∽△HMG．
∴
．
在Rt△GME中，
∴tan∠MEG=
=
．
∴∠MEG=60°．
由（1）得△AEM≌△DFM．
∴ME=MF．
∵MG⊥EF， ∴GE=GF．
∴△GEF是等边三角形． 9分
