题目内容
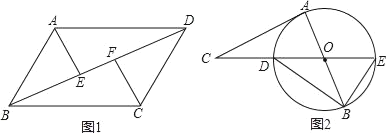
【题目】如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当CF=DE时,∠DOF的大小是_____.
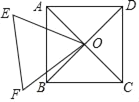
【答案】165°或15°.
【解析】
如图1,连结CF、DE,根据正方形与等边三角形的性质得OC=OD,∠COD=90°,OE=OF,∠EOF=60°,根据“SSS”可判断△ODE≌△OCF,则∠DOE=∠COF,于是可求∠DOF;如图2,同理可证得△ODE≌△OCF,所以∠DOE=∠COF,于是可求∠DOF.
解:如图1,连结CF、DE,
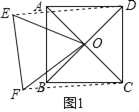
∵四边形ABCD为正方形,
∴OC=OD,∠COD=90°,
∵△OEF为等边三角形,
∴OE=OF,∠EOF=60°,
在△ODE和△OCF中
 ,
,
∴△ODE≌△OCF(SSS),
∴∠DOE=∠COF=![]() ×(360°﹣90°﹣60°)=105°,
×(360°﹣90°﹣60°)=105°,
∴∠DOF=∠DOE+60°=165°;
如图2,
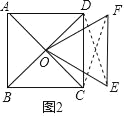
在△ODE和△OCF中,
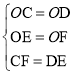 ,
,
∴△ODE≌△OCF(SSS),
∴∠DOE=∠COF,
∴∠DOF=∠COE,
∴∠DOF=![]() ×(90°﹣60°)=15°.
×(90°﹣60°)=15°.
∴∠DOF的大小是165°或15°.
故答案为:165°或15°.

【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
①填空:此次试验中“5点朝上”的频率为____;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图的方法加以说明,并求出其最大概率
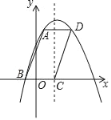
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
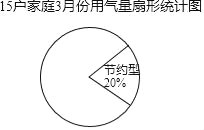
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.