题目内容
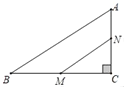
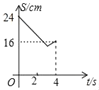
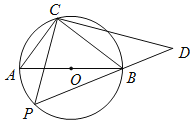
【题目】![]() 是⊙O直径,在
是⊙O直径,在![]() 的异侧分别有定点
的异侧分别有定点![]() 和动点
和动点![]() ,如图所示,点
,如图所示,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() ,交
,交![]() 的延长线于
的延长线于![]() ,已知
,已知![]() ,
,![]() ∶
∶![]() =
=![]() ∶
∶![]() .
.
(1)求证:![]() ·
·![]() =
=![]() ·
·![]() ;
;
(2)当点![]() 运动到
运动到![]() 弧的中点时,求
弧的中点时,求![]() 的长;
的长;
(3)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?请直接写出这个最大面积.
的面积最大?请直接写出这个最大面积.

【答案】(1)证明见解析;(2)CD=![]() ;(3)当PC为⊙O直径时,△PCD的最大面积=
;(3)当PC为⊙O直径时,△PCD的最大面积=![]() .
.
【解析】
(1)由圆周角定理可得∠PCD=∠ACB=90°,可证△ABC∽△PCD,可得![]() ,即可得证。
,即可得证。
(2)由题意可求BC=4,AC=3,由勾股定理可求CE的长,由锐角三角函数可求PE的长,即可得PC的长,由ACCD=PCBC可求CD的值;
(3)当点P在![]() 上运动时,
上运动时,![]() ,由(1)可得:
,由(1)可得:![]() ,可得
,可得![]() ,当PC最大时,△PCD的面积最大,而PC为直径时最大,故可求解.
,当PC最大时,△PCD的面积最大,而PC为直径时最大,故可求解.
证明:(1)
∵AB为直径,
∴∠ACB=90°
∵PC⊥CD,
∴∠PCD=90°
∴∠PCD=∠ACB,且∠CAB=∠CPB
∴△ABC∽△PCD
∴![]()
∴ACCD=PCBC
(2)∵AB=5,BC:CA=4:3,∠ACB=90°
∴BC=4,AC=3,
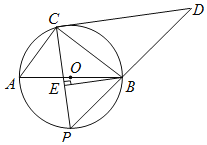
当点P运动到![]() 的中点时,过点B作BE⊥PC于点E
的中点时,过点B作BE⊥PC于点E
∵点P是![]() 的中点,
的中点,
∴∠PCB=45°,且BC=4
∴CE=BE=![]() BC=2
BC=2![]()
∵∠CAB=∠CPB
∴tan∠CAB=![]() =tan∠CAB=
=tan∠CAB=![]()
∴PE=![]()
∴PC=PE+CE=![]() +2
+2![]() =
=![]()
∵ACCD=PCBC
∴3×CD=![]() ×4
×4
∴CD=![]()
(3)当点P在![]() 上运动时,S△PCD=
上运动时,S△PCD=![]() ×PC×CD,
×PC×CD,
由(1)可得:CD=![]() PC
PC
∴S△PCD=![]() =
=![]() PC2,
PC2,
∴当PC最大时,△PCD的面积最大,
∴当PC为⊙O直径时,△PCD的最大面积=![]() ×52=
×52=![]()

【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?