题目内容
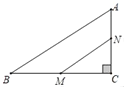
【题目】如图,在△ABC中,∠C=90°,AB=10cm,cosB=![]() 点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
A.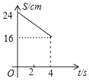 B.
B.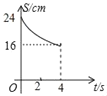 C.
C.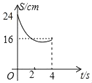 D.
D.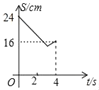
【答案】C
【解析】
在△ABC中,∠C=90°,AB=10cm,cosB=![]() ,可以分别求出BC,AC的长,用含t的代数式表示出NC和MC,然后用三角形ABC的面积减去三角形MNCde面积,即可表示出四边形ABMN的面积为S,结合图象可以判断选项.
,可以分别求出BC,AC的长,用含t的代数式表示出NC和MC,然后用三角形ABC的面积减去三角形MNCde面积,即可表示出四边形ABMN的面积为S,结合图象可以判断选项.
解:∵在△ABC中,∠C=90°,AB=10cm,cosB=![]() ,
,
∴BC=8,AC=6,
t秒后,NC=6﹣t,MC=2t,
∴S=S△ABC﹣S△MNC=![]() =(t﹣3)2+15,
=(t﹣3)2+15,
从图象来看,排除选项A和D,
∵当t=2时,y=16故B不符合要求,C符合.
故选C.

练习册系列答案
相关题目