��Ŀ����
����Ŀ�����ǹ涨���Զ��κ���y=ax2+bx+c�Ķ�����ϵ��a��2��Ϊһ����ϵ����һ����ϵ��bΪ��������һ�κ���y=2ax+b�������κ���y=ax2+bx+c�����Ӻ������������������κ���y=ax2+bx+c����һ�κ���y=2ax+b����ĸ��������
��1����һ�κ���y=2x-4�Ƕ��κ���y=ax2+bx+c�����Ӻ��������Ҷ��κ��������㣨3��0������˶��κ����Ľ���ʽ���������꣮
��2�������Ӻ�����y=x-6����ĸ����������СֵΪ1������ĸ�������ĺ�������ʽ��
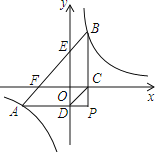
��3����֪���κ���y=-x2-4x+8�����Ӻ�����ͼ��ֱ��l��x�ᡢy�ύ��C��D���㣬����PΪ���κ���y=-x2-4x+8�Գ����Ҳ��ϵĶ��㣬����PCD����������ֵ��
���𰸡�(1) ![]() �������ߵĶ�������Ϊ
�������ߵĶ�������Ϊ![]() �� (2) ��ĸ�������ĺ�������ʽΪ
�� (2) ��ĸ�������ĺ�������ʽΪ![]() ��(3)��
��(3)��![]() ʱ��
ʱ��![]() ������ֵΪ
������ֵΪ![]() ��
��
��������
(1)���ݶ��κ���y=ax2+bx+c�ġ��Ӻ������Ķ��壬��֪a=1��b=-4���ٰѵ㣨3��0���������ʽ���ɽ�����⣮
��2�����Ӻ�����![]() �ġ�ĸ������Ϊ
�ġ�ĸ������Ϊ![]() ��������СֵΪ1�������C��ֵ��
��������СֵΪ1�������C��ֵ��
��3����ֱ��![]() �ı���ʽΪ
�ı���ʽΪ![]() ������C,D����,�ٸ���
������C,D����,�ٸ���![]() �ɽ�����⣮
�ɽ�����⣮
(1)�������![]() ��
��![]() ��
��
�������ߵĽ���ʽΪ![]() ���ѵ�
���ѵ�![]() ����ɵ�
����ɵ�![]() ��
��
�������ߵĽ���ʽΪ![]() ��
��
��![]() ��
��
�������ߵĶ�������Ϊ![]() ��
��
(2)���Ӻ�����![]() �ġ�ĸ������Ϊ
�ġ�ĸ������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ࡰĸ�������ĺ�������ʽΪ![]() ��
��
(3)��ͼ������![]() ����
����![]() �������Ϊ
�������Ϊ![]() ��
��
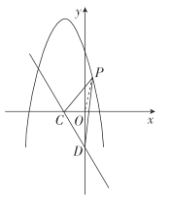
�������ֱ��![]() �ı���ʽΪ
�ı���ʽΪ![]() ��
��
��![]() ��
��![]() ��
��
��![]()
![]() ��
��
�൱![]() ʱ��
ʱ��![]() ������ֵΪ
������ֵΪ![]() ��
��