题目内容
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC>BC,分别以AB,BC,CA为一边向△ABC外作正方形ABDE、BCMN,CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3.
(1)猜想S1、S2、S3的大小关系.
(2)请对(1)的猜想,任选一个关系进行证明;
(3)若将图1中的Rt△ABC改为图2中的任意△ABC,若SABC=5,求出S1+S2+S3的值;
(4)若将图2中的任意△ABC改为任意凸四边形ABCD,若S△AEG+S△CNK+S△IBH+S△DFM=α,则四边形ABCD的面积为 (直接用含α的代数式表示结果)

【答案】(1)S1=S2=S3(2)见解析(3)15(4)![]() a
a
【解析】
(1)猜想三个三角形面积相等;
(2)证明三个三角形都与△ABC面积相等.观察图形,要证明面积相等,图中正方形提供了一组相等的边作为底,只要证明高相等即可;
(3)证明思路同(2),S1、S2、S3面积都等于△ABC问题可求;
(4)作四边形ABCD对角线,可以以利用(3)中结论,△AEG、△CNK、△IBH、△DFM的面积可以分别于四边形ABCD被对角线分割所得的三角形对应相等,则问题可证.
(1)猜想:S1=S2=S3
(2)如图1,延长FA,过点E作EH⊥FA于H,
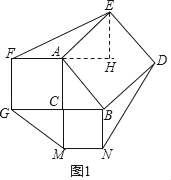
由已知:∠BAE=∠CAH=90°,
∴∠CAB=∠HAE.
∵∠ACB=∠AHE=90°,AE=AB,
∴△HAE≌△CAB,
∴EH=BC,
∴S△AEF=![]() =
=![]() =S△ABC,
=S△ABC,
∴S1=S△ABC,
同理:S2=S△ABC,S3=S△ABC,
∴S1=S2=S3
(3)如图2
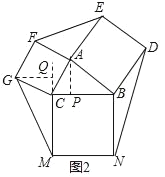
分别过点G和A作GQ⊥MC于Q,AP⊥BC于P,
由已知:∠GCA=∠QCB=90°,
∴∠GCQ=∠ACP.
又∵∠GQC=∠APC=90°,
GC=AC,
∴△GCQ≌△ACP,
∴GQ=AP,
∵S△GCM=![]() ,
,
S△ABC=![]() ,
,
MC=BC,
∴S△GCM=S△ABC,
∴S3=S△ABC,
同理:S1=S△ABC,
S2=S△ABC,
∴S1=S2=S3=S△ABC,
∵SABC=5,
∴S1+S2+S3=15;
(4)如图3,连AC,
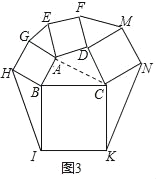
由(3)可知,S△DFM=S△ADC,
S△IBH=S△ABC,
∴S△DFM+S△IBH=S△ADC+S△ABC=S四边形ABCD,
同理:S△AEG+S△CNK=S四边形ABCD,
∴S△AEG+S△CNK+S△IBH+S△DFM=2S四边形ABCD,
∵S△AEG+S△CNK+S△IBH+S△DFM=α,
∴2S四边形ABCD=α,
∴四边形ABCD的面积为![]() ,
,
故答案为:![]()