Question

【题目】如图，点P在以AB为直径的半圆内，连AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法正确的是:

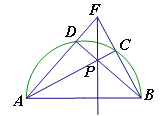
①AC垂直平分BF；②AC平分∠BAF；③PF⊥AB；④BD⊥AF.

A．①② B．①④ C．②④ D．③④

Answer 1

【答案】D．

【解析】

试题①∵AB为直径，

∴∠ACB=90°，

∴AC垂直BF，但不能得到AC平分BF，

故①错误；

②假设AC平分∠BAF，我们有：∠CAB=∠CAF，由①知：AC垂直BF，∴∠ACB=∠ACF=90°，∴∠ACB-∠CAB=∠ACF-∠CAF，即：∠ ABC=∠AFC，从而得到△ABF是等腰三角形。又因为AC垂直BF，根据等腰三角形的三线合一知：AC平分BF，这与①不能得到AC平分BF相矛盾。

故②错误；

③∵AB为直径，

∴∠ACB=90°，∠FPD=90°，

∵三角形的三条高线所在的直线交于一点，

∴FP⊥AB，

故③正确；

④∵AB为直径，

∴∠ADB=90°，

∴BD⊥AF．

故④正确，

综上所述只有③④正确，

故选D．