题目内容
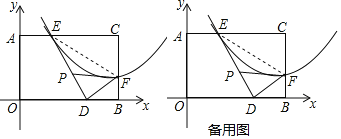
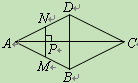
【题目】如图,四边形![]() 是矩形纸片,
是矩形纸片,![]() .对折矩形纸片
.对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ;展平后再过点
;展平后再过点![]() 折叠矩形纸片,使点
折叠矩形纸片,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕
,折痕![]() 与
与![]() 相交于点
相交于点![]() ;再次展平,连接
;再次展平,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④△
;④△![]() 是等边三角形; ⑤
是等边三角形; ⑤![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是( ).
.其中正确结论的序号是( ).
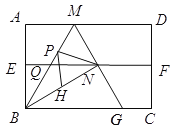
A. ①②④B. ①④⑤C. ①③④D. ①②③⑤
【答案】B
【解析】
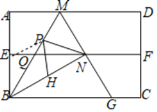
先证明BN=2BE,推出∠ENB=30°,∠ABN=60°,△BMG为等边三角形,可计算出AM、QN的长度。H关于BM的对称点是E,![]() 的最小值即为EN的长度。一一判断即可.
的最小值即为EN的长度。一一判断即可.
解:在Rt△BEN中,∵BN=AB=2BE,
∴∠ENB=30°,
∴∠ABN=60°,故①正确,
∴∠ABM=∠NBM=∠NBG=30°,
∴AM=ABtan30°=![]() ,故②错误,
,故②错误,
∵∠AMB=∠BMN=60°,
∵AD∥BC,
∴∠GBM=∠AMB=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,故④正确.
∴BG=BM=2AM=![]() ,
,
∵EF∥BC∥AD,AE=BE,
∴BQ=QM,MN=NG,
∴QN是△BMG的中位线,
∴QN=![]() BG=
BG=![]() ,故③不正确.
,故③不正确.
连接PE.∵BH=BE=1,∠MBH=∠MBE,
∴E、H关于BM对称,
∴PE=PH,
∴PH+PN=PE+PN,
∴E、P、N共线时,PH+PN的值最小,最小值=EN=![]() ,故⑤正确,
,故⑤正确,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目