��Ŀ����
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
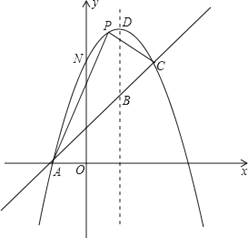
��1��������ֱ��AC�ĺ�����ϵʽ��
��2�����M��3��m������ʹMN+MD��ֵ��Сʱm��ֵ��
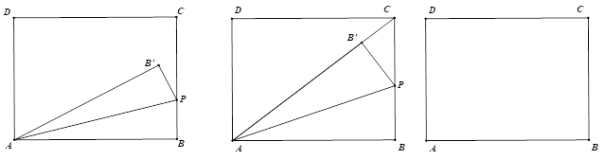
��3���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�B��EΪֱ��AC�ϵ�����һ�㣬����E��EF��BD���������ڵ�F����B��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�
��4����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ��
���𰸡���1��![]() ��ֱ��AC�ĺ�����ϵʽΪy=x+1��2��
��ֱ��AC�ĺ�����ϵʽΪy=x+1��2��![]() ��3����2��3������0��1����
��3����2��3������0��1����![]() ��
��![]() ����4��
����4��![]()
��������
�⣺��1����������y=��x2+bx+c����A����1��0����C��2��3���ã�
![]() �����
�����![]() ���������ߵĺ�����ϵʽΪ
���������ߵĺ�����ϵʽΪ![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy=kx+n����ֱ��AC����A����1��0����C��2��3����
![]() �����
�����![]() ����ֱ��AC�ĺ�����ϵʽΪy=x+1��
����ֱ��AC�ĺ�����ϵʽΪy=x+1��
��2����N�����ֱ��x=3�ĶԳƵ�N����

��x=0����y=3����N��0��3����
��N����6�� 3��
��![]() ��
��
D��1��4����
��ֱ��DN���ĺ�����ϵʽΪy=sx+t����
![]() �����
�����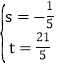 ��
��
����ֱ��DN���ĺ�����ϵʽΪ![]() ��
��
������ԳƵ����ʺ����������߹�ϵ��֪��M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��![]() ��
��
��ʹMN+MD��ֵ��Сʱm��ֵΪ![]() ��
��
��3���ɣ�1������2����D��1��4����B��1��2����
����BDΪƽ���ı��ζԽ���ʱ����B��C��D��N������֪���ı���BCDN��ƽ���ı��Σ���ʱ����E���C�غϣ���E��2��3����
����BDΪƽ���ı��α�ʱ��
����E��ֱ��AC�ϣ�����E��x��x+1������F��x��![]() ����
����
����BD=2
�����ı���BDEF��BDFE��ƽ���ı���ʱ��BD=EF��
��![]() ����
����![]() ��
��
��![]() ����ã�x=0��x=1����ȥ������E��0��1����
����ã�x=0��x=1����ȥ������E��0��1����
��![]() ����ã�
����ã�![]() ����E
����E![]() ��E
��E![]() ��
��
���ϣ����������ĵ�EΪ��2��3������0��1����![]() ��
��![]() ��
��
��4����ͼ������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G��

��Q��x��x+1������P��x����x2+2x+3����
��![]() ��
��
��![]()
![]() ��
��
��![]() ��
��
����![]() ʱ����APC�����ȡ�����ֵ�����ֵΪ
ʱ����APC�����ȡ�����ֵ�����ֵΪ![]() ��
��
��1�����ô���ϵ��������κ�������ʽ��һ�κ�������ʽ��
��2��������ԳƵ����ʺ����������߹�ϵ��N�����ֱ��x=3�ĶԳƵ�N������M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��3����BDΪƽ���ı��ζԽ��ߺ�BDΪƽ���ı��α�����������ۡ�
��4����ͼ������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G����Q��x��x+1������P��x����x2+2x+3��������߶�PQ=��x2+x+2����ͼʾ�Լ������ε������ʽ֪![]() ���ɶ��κ�������ֵ����֪��APC����������ֵ��
���ɶ��κ�������ֵ����֪��APC����������ֵ��