Ő‚ńŅńŕ»›
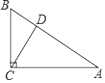
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ≥§∑Ĺ–ő![]() ÷–£¨BC=3£¨∂ĮĶ„
÷–£¨BC=3£¨∂ĮĶ„![]() ī”
ī”![]() ≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»£¨—ō…šŌŖ
≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»£¨—ō…šŌŖ![]() ∑ĹŌÚ“∆∂Į£¨◊ų
∑ĹŌÚ“∆∂Į£¨◊ų![]() Ļō”ŕ÷ĪŌŖ
Ļō”ŕ÷ĪŌŖ![]() Ķń∂‘≥∆
Ķń∂‘≥∆![]() £¨…ŤĶ„
£¨…ŤĶ„![]() Ķń‘ň∂Į Īľšő™
Ķń‘ň∂Į Īľšő™![]()
£®1£©ĶĪPĶ„‘ŕŌŖ∂őBC…Ō«“≤Ľ”ŽCĶ„÷ōļŌ Ī£¨»Ű÷ĪŌŖPB°Į”Ž÷ĪŌŖCDŌŗĹĽ”ŕĶ„M£¨«“°ŌPAM=45°„£¨ ‘«ů£ļABĶń≥§
£®2£©»ŰAB=4
ĘŔ»ÁÕľ2£¨ĶĪĶ„B°Į¬š‘ŕAC…Ō Ī£¨Ō‘»Ľ°ųPCB°Į «÷ĪĹ«»żĹ«–ő£¨«ůīň ĪtĶń÷Ķ
Ęŕ «∑Ůīś‘ŕ“ž”ŕÕľ2Ķń ĪŅŐ£¨ ĻĶ√°ųPCB°Į «÷ĪĹ«»żĹ«–ő£Ņ»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥Ųňý”–∑ŻļŌŐ‚“‚ĶńtĶń÷Ķ£Ņ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…

°ĺīūįł°Ņ£®1£©ABĶń≥§ő™3£Ľ£®2£©ĘŔ![]() £ĽĘŕtĶń÷Ķő™
£ĽĘŕtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() ĽÚ4.
ĽÚ4.
°ĺĹ‚őŲ°Ņ
£®1£©»ÁÕľňý ĺ£¨—”≥§![]() ”ŽCDĹĽ”ŕM£¨Ń¨Ĺ”AM£¨”√Ĺ«Ĺ«ĪŖ÷§√ų
”ŽCDĹĽ”ŕM£¨Ń¨Ĺ”AM£¨”√Ĺ«Ĺ«ĪŖ÷§√ų![]() £¨Ņ…Õ∆≥ŲAB=BC=3.
£¨Ņ…Õ∆≥ŲAB=BC=3.
£®2£©ĘŔ‘ŕRt°ų![]() ÷–£¨’“≥ŲĪŖ≥§ņŻ”√ĻīĻ…∂®ņŪĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚£Ľ
÷–£¨’“≥ŲĪŖ≥§ņŻ”√ĻīĻ…∂®ņŪĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚£Ľ
Ęŕ∑÷»ż÷÷«ťŅŲŐ÷¬Ř£ļ![]() £¨
£¨![]() £¨
£¨![]() £¨∑÷Īū◊ų≥ŲŌŗ”¶ĶńÕľ–ő£¨‘ŕ
£¨∑÷Īū◊ų≥ŲŌŗ”¶ĶńÕľ–ő£¨‘ŕ![]() ÷–£¨∑÷Īū’“≥ŲĪŖ≥§£¨ņŻ”√ĻīĻ…∂®ņŪĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚.
÷–£¨∑÷Īū’“≥ŲĪŖ≥§£¨ņŻ”√ĻīĻ…∂®ņŪĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚.
£®1£©»ÁÕľňý ĺ£¨—”≥§![]() ”ŽCDĹĽ”ŕM£¨Ń¨Ĺ”AM£¨
”ŽCDĹĽ”ŕM£¨Ń¨Ĺ”AM£¨

”…’ŘĶĢĶń–‘÷ Ņ…÷™![]() £¨
£¨![]() £¨
£¨![]()
°Ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]()
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨

°ŗ![]() °’
°’![]() £®AAS£©
£®AAS£©
°ŗ![]()
”÷°ŖABCDő™ĺō–ő£¨°ŗAD=BC=3£¨
°ŗAB=3
£®2£©ĘŔ‘ŕRt°ųABC÷–£¨![]()
°ŖĶ„PĶ„Ķń‘ň∂Į Īľšő™t£¨ňŔ∂»ő™1£¨°ŗBP=t£¨
![]() £¨
£¨![]() £¨
£¨![]() ,
,
‘ŕRt°ų![]() ÷–£¨”…ĻīĻ…∂®ņŪ”–
÷–£¨”…ĻīĻ…∂®ņŪ”–![]() £¨ľī
£¨ľī![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() .
.
ĘŕĶĪ![]() £¨»ÁŌ¬Õľňý ĺ£¨
£¨»ÁŌ¬Õľňý ĺ£¨

°ŖňńĪŖ–őABCDő™ĺō–ő£¨°ŗAD=BC=3£¨CD=AB=4£¨
”–’ŘĶĢ–‘÷ ”–![]() £¨‘ŕRt°ų
£¨‘ŕRt°ų![]() ÷–£¨
÷–£¨
![]() £¨
£¨
°ŗ![]()
‘ŕRt°ų![]() ÷–£¨
÷–£¨![]() £¨
£¨![]()
![]() £¨ľī
£¨ľī![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]()
ĶĪ°Ō![]() =90°„ Ī£¨»ÁŌ¬Õľňý ĺ£¨
=90°„ Ī£¨»ÁŌ¬Õľňý ĺ£¨

”…’ŘĶĢŅ…Ķ√![]() £¨
£¨
‘ŕRt°ų![]() ÷–£¨
÷–£¨![]()
‘ŕRt°ų![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]()
![]() £¨ľī
£¨ľī![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]()
ĶĪ![]() =90°„ Ī£¨»ÁŌ¬Õľňý ĺ£¨łýĺ›’ŘĶĢ“◊Ķ√ňńĪŖ–ő
=90°„ Ī£¨»ÁŌ¬Õľňý ĺ£¨łýĺ›’ŘĶĢ“◊Ķ√ňńĪŖ–ő![]() ő™’ż∑Ĺ–ő£¨°ŗPB=AB=4
ő™’ż∑Ĺ–ő£¨°ŗPB=AB=4

◊Ř…Ō£¨¬ķ◊„Ő‚“‚ĶńtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() ĽÚ4.
ĽÚ4.

 ļģľŔņ÷‘įĪĪĺ©ĹŐ”ż≥Ųįś…ÁŌĶŃ–īūįł
ļģľŔņ÷‘įĪĪĺ©ĹŐ”ż≥Ųįś…ÁŌĶŃ–īūįł