题目内容
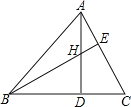
【题目】如图,在![]() 中,
中,![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,抛物线
轴的负半轴上,抛物线![]() 经过点
经过点![]() 和点
和点![]()

![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 在抛物线的对称轴上是否存在点
在抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
![]() 点
点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,探究:当点
,探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形,此时,请判断四边形
是平行四边形,此时,请判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)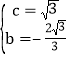 ;(2)符合题意的
;(2)符合题意的![]() 点的坐标为:
点的坐标为:![]() ;
;![]() ;
;![]() ;
;![]() ,
,![]() ;(3)四边形
;(3)四边形![]() 是梯形,理由见解析.
是梯形,理由见解析.
【解析】
(1)直接利用待定系数法求出抛物线解析式得出即可;
(2)利用当AQ=QC,以及当AC=Q1C时,当AC=CQ2=2![]() 时,当AQ3=AC=2
时,当AQ3=AC=2![]() 时,分别得出符合题意的答案即可;
时,分别得出符合题意的答案即可;
(3)利用平行四边形的性质首先得出BC的长,进而表示出线段ME的长,进而求出答案,再利用梯形的判定得出答案.
![]() ∵点
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,抛物线
轴的负半轴上,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴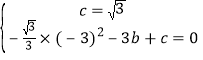 ,
,
解得: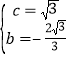 ;
;
![]() 在抛物线的对称轴上存在点
在抛物线的对称轴上存在点![]() ,使得
,使得![]() 为等腰三角形,
为等腰三角形,
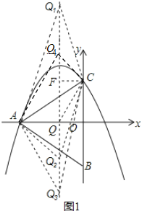
当![]() ,如图
,如图![]() ,
,
由![]() 得:
得:![]() ,
,
即抛物线对称轴为:直线![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
当![]() 时,过点
时,过点![]() 作
作![]() 直线
直线![]() ,于一点
,于一点![]() ,
,
则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故
,故![]() 的坐标为:
的坐标为:![]() ;
;
当![]() 时,由
时,由![]() 的坐标可得;
的坐标可得;![]() ;
;
当![]() 时,则
时,则![]() ,故
,故![]() ,根据对称性可知
,根据对称性可知![]() (
(![]() 和
和![]() 关于
关于![]() 轴对称)也符合题意,
轴对称)也符合题意,
综上所述:符合题意的![]() 点的坐标为:
点的坐标为:![]() ;
;![]() ;
;![]() ;
;![]() ,
,![]() ;
;
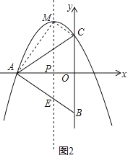
![]() 如图
如图![]() 所示,当四边形
所示,当四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
∵![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
∴![]() ,
,
则![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
故![]() ,
,
解得: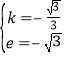 ,
,
故直线![]() 的解析式为:
的解析式为:![]() ,
,
设![]() ,
,![]() ,
,
故![]() ,
,
解得:![]() (不合题意舍去),
(不合题意舍去),![]() ,
,
故![]() 点在
点在![]() ,此时四边形
,此时四边形![]() 是平行四边形;
是平行四边形;
四边形![]() 是梯形,
是梯形,
理由:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,![]() ,
,
∴四边形![]() 是梯形.
是梯形.

练习册系列答案
相关题目