Question

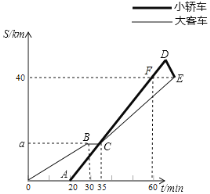
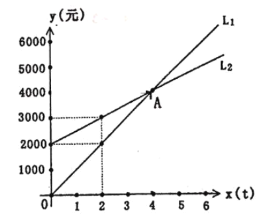
【题目】如图，L1反映了某公司产品的销售收入（元）与销售量的函数关系，L2反映了该公司产品的销售成本（元）与销售量的函数关系，根据图象解答问题：

（1）分别求出销售收入和销售成本与的函数关系式

（2）指出两图象的交点的实际意义，公司的销售量至少要达到多少才能不亏损？

（3）如果该公司要盈利1万元，需要销售多少吨产品？

Answer 1

【答案】（1），；（2）交点A的实际意义是销售收入等于销售成本，即不盈利也不亏损；公司的销售量至少要达到4t才能不亏损；（3）如果该公司要盈利1万元，需要销售24吨产品.

【解析】

（1）分别利用待定系数法求与的函数关系式即可；

（2）由表示销售收入，表示销售成本可知交点A的实际意义是销售收入等于销售成本，即不盈利也不亏损；求出交点横坐标，根据函数图象可得到何时不亏损；

（3）根据“盈利＝销售收入－销售成本”列式计算即可.

解：（1）设，

由函数图象得：过点（2，2000），则，

解得：，

∴；

设，

由函数图象得：过点（0，2000），（2，3000），则，

解得：，

∴；

（2）由题意得：交点A的实际意义是销售收入等于销售成本，即不盈利也不亏损；

当时，即，

解得：x=4，即A点横坐标为4，

由函数图象可得，当x≥4时，，

∴公司的销售量至少要达到4t才能不亏损；

（3）由题意得：，即，

解得：，

答：如果该公司要盈利1万元，需要销售24吨产品.