题目内容
【题目】如图,![]() 是矩形
是矩形![]() 内一点,
内一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

![]() 请判断四边形
请判断四边形![]() 是否是正方形?若是,写出证明过程:若不是,说明理由;
是否是正方形?若是,写出证明过程:若不是,说明理由;
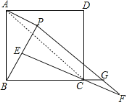
![]() 延长
延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的度数.
的度数.
【答案】![]() 四边形
四边形![]() 为正方形,理由见解析;(2)
为正方形,理由见解析;(2)![]()
【解析】
(1)由四边形ABCD为矩形可得∠ABC=90°,易得∠ABP+∠PBC=90°,由AP⊥BP,可得∠ABP+∠PAB=90°,易得∠PBC=∠PAB,由AAS定理可得△ABP≌△BCE,由全等三角形的性质可得AB=BC,易得结论;
(2)连接AC,由△ABP≌△BCE易得AP=BE,又CF=BE,可得AP=CF,易得四边形ACGP是平行四边形,可得∠ACB=∠BGC,由四边形ABCD是正方形,AC是对角线,可得∠ACB=∠BGP=45°.
解:![]() 四边形
四边形![]() 为正方形.
为正方形.
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
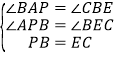 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴矩形![]() 为正方形;
为正方形;
![]() 连接
连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,![]() 是对角线,
是对角线,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目