题目内容
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
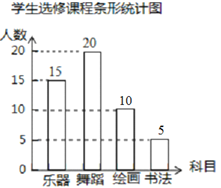
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
【答案】(1)50;![]() (2)选修绘画的人数为10人,选修书法的人数为5人,条形统计图见解析; (3)该校约有600人选修乐器课程.
(2)选修绘画的人数为10人,选修书法的人数为5人,条形统计图见解析; (3)该校约有600人选修乐器课程.
【解析】
(1)根据选修舞蹈的人数与所占的百分比列式计算即可求得参加调查的学生总人数,然后用选修乐器的人数除以参加调查的学生总人数得到m的值;
(2)用参加调查的学生总人数分别乘以选修绘画和书法的所占百分比即可得到相应的人数,然后补全条形统计图即可;
(3)用学生总数2000人乘以选修乐器所占百分比,即可得到答案.
(1)根据选修舞蹈的人数和所占百分比得:
本次调查的学生共有![]() 人
人![]() ,
,
∴![]() ;
;
故答案为:50;![]() ;
;
![]() 选修绘画的人数
选修绘画的人数![]() 人
人![]() ,选修书法的人数
,选修书法的人数![]() 人
人![]() ,
,
如图所示:
![]() 估计该校选修乐器课程的人数为
估计该校选修乐器课程的人数为![]() (人).
(人).
答:该校约有600人选修乐器课程.

 阅读快车系列答案
阅读快车系列答案【题目】背景阅读:
意大利著名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为裴波那契数列.
实践操作:
(1)写出裴波那契数列的前10个数;
(2)裴波那契数列的前2017个数中,有多少个奇数?
(3)现以这组数的各个数作为正方形的边长构造如图1的正方形系列:再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④、⑤……


(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号 | ① | ② | ③ | ④ | ⑤ | …… |
周长 | 6 | 10 | …… |
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形的面积和周长.






