题目内容
在半径为4的⊙O中,点C是以AB为直径的半圆的中点,OD⊥AC,垂足为D,点E是射线AB上的任意一点,DF//AB,DF与CE相交于点F,设EF= ,DF=
,DF= .
.
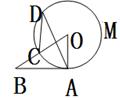
(1) 如图1,当点E在射线OB上时,求 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;

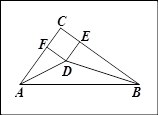
(2) 如图2,当点F在⊙O上时,求线段DF的长;

(3) 如果以点E为圆心、EF为半径的圆与⊙O相切,求线段DF的长.
 ,DF=
,DF= .
. (1) 如图1,当点E在射线OB上时,求
 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;
(2) 如图2,当点F在⊙O上时,求线段DF的长;

(3) 如果以点E为圆心、EF为半径的圆与⊙O相切,求线段DF的长.
(1)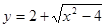 (
(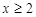 );(2)2+2
);(2)2+2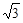 ;(3)
;(3)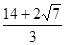 或
或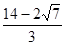 或
或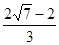
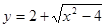 (
(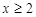 );(2)2+2
);(2)2+2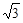 ;(3)
;(3)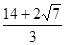 或
或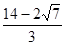 或
或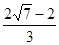
试题分析:(1)连接OC,先根据垂径定理证得OD=AD,再结合DF//AB可得CF=EF,即可得到DF=
 =
=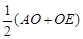 .由点C是以AB为直径的半圆的中点,可得CO⊥AB.由EF=
.由点C是以AB为直径的半圆的中点,可得CO⊥AB.由EF=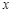 ,AO=CO=4,可得到CE=2
,AO=CO=4,可得到CE=2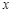 ,OE=
,OE=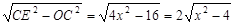 ,即可得到结果;
,即可得到结果;(2)当点F在⊙O上时,连接OC、OF,则EF=
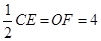 ,即得OC=OB=
,即得OC=OB=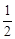 AB=4,从而可以求得结果;
AB=4,从而可以求得结果;(3)分当⊙E与⊙O外切于点B时,当⊙E与⊙O内切于点B时,当⊙E与⊙O内切于点A时,三种情况,根据勾股定理列方程求解即可.
(1)连接OC
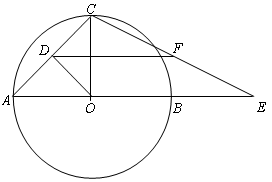
∵AC是⊙O的弦,OD⊥AC,
∴OD=AD.
∵DF//AB,
∴CF=EF,
∴DF=
 =
=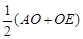 .
.∵点C是以AB为直径的半圆的中点,
∴CO⊥AB.
∵EF=
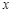 ,AO=CO=4
,AO=CO=4∴CE=2
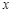 ,OE=
,OE=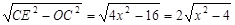 .
.∴
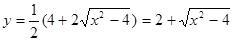 (
(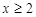 ).
).(2)当点F在⊙O上时,连接OC、OF,EF=
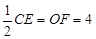 ,
,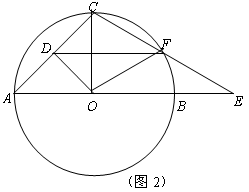
∴OC=OB=
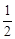 AB=4.
AB=4.∴DF=2+
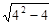 =2+2
=2+2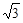 .
.(3)当⊙E与⊙O外切于点B时,BE=FE.
∵
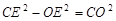 ,
,∴
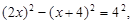
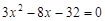 ,
,∴

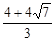 ,
,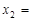
 ).
).∴DF=
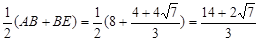 .
.当⊙E与⊙O内切于点B时,BE=FE.
∵
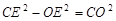 ,
,∴
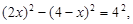
 ,
,∴

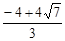 ,
,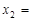
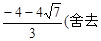 ).
).∴DF=
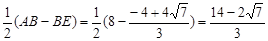 .
.当⊙E与⊙O内切于点A时,AE=FE.
∵
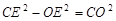 ,
,∴
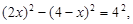
 ,
,∴

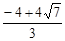 ,
,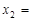
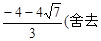 ).
).∴DF=
 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目

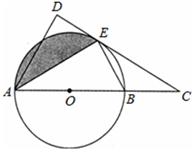
 为圆心,
为圆心, 为半径的扇形中,圆心角
为半径的扇形中,圆心角 ,另一个扇形是以点
,另一个扇形是以点 为圆心,
为圆心, 为半径,圆心角
为半径,圆心角 ,点
,点 ,如图.如果两个扇形的圆弧部分(弧
,如图.如果两个扇形的圆弧部分(弧 和弧CD)相交,那么实数
和弧CD)相交,那么实数
 、
、 ,
, ,则
,则 的度数为( )
的度数为( )
 B.
B. C.
C. D.
D.