Question

如图，在△ABC中，∠C＝90°，∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F，

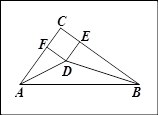
（1）求证：四边形CFDE是正方形
（2）若AC＝3，BC＝4，求△ABC的内切圆半径.

Answer 1

可证DE=DG∴DE=DF∵∠C=∠CFD=∠CED=90°∴四边形CFDE是正方形.
（2）△ABC的内切圆半径为1.

试题分析：（1）过D作DG⊥AB交AB于G点，
∵AD是∠BAC的角平分线
∴∠FAD=∠BAD
∵DF⊥AC,DG⊥AB
∴∠AFD=∠AGD=90°
∵AD=AD
∴△AFD≌△AGD
∴DF=DG
同理可证DE=DG
∴DE=DF
∵∠C=∠CFD=∠CED=90°
∴四边形CFDE是正方形.  
（2）．∵AC＝3，BC＝4
∴AB=5
由（1）知AF=AG,BE=BG
∴AF+BE=AB
∵四边形CFDE是正方形∴2CE=AC+CB-AB=2，即CE=1
△ABC的内切圆半径为1.
点评：本题难度中等，主要考查学生对正方形的判定与内切圆知识点的掌握。为中考常考题型，学生要牢固掌握几何性质与判定。