题目内容
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
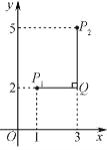
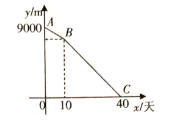
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
【答案】(1)(10,7500)(2)直线BC的解析式为y=-250x+10000,自变量x的取值范围为10≤x≤40.(3)1250米.
【解析】
(1)由于前面10天由甲单独完成,用总的长度减去已完成的长度即为剩余的长度,从而求出点B的坐标;(2)利用待定系数法求解即可;(3)已队工作25天后,即甲队工作了35天,故当x=35时,函数值即为所求.
(1)9000-150×10=7500.
∴点B的坐标为(10,7500)
(2)设直线BC的解析式为y=kx+b,依题意,得:
解得:
∴直线BC的解析式为y=-250x+10000,
∵乙队是10天之后加入,40天完成,
∴自变量x的取值范围为10≤x≤40.
(3)依题意,当x=35时,y=-250×35+10000=1250.
∴乙队工作25天后剩余管线的长度是1250米.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目