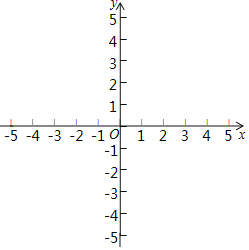题目内容
【题目】如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=![]() x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═
x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═![]() x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=
x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=![]() x于点B3;……按如此规律进行下去,点B2020的坐标为_____.
x于点B3;……按如此规律进行下去,点B2020的坐标为_____.

【答案】(22020,22019)
【解析】
根据题意可以求得点B1的坐标,点A2的坐标,点B2的坐标,然后即可发现坐标变化的规律,从而可以求得点B2020的坐标.
解:由题意可得,点A1的坐标为(1,2),
设点B1的坐标为(a,![]() a),
a),
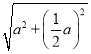 =
=![]() ,解得,a=2,
,解得,a=2,
∴点B1的坐标为(2,1),
同理可得,点A2的坐标为(2,4),点B2的坐标为(4,2),
点A3的坐标为(4,8),点B3的坐标为(8,4),
……
∴点B2020的坐标为(22020,22019),
故答案为:(22020,22019).

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目