题目内容
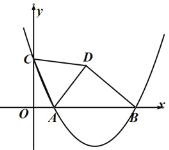
【题目】如图平面直角坐标系,已知二次函数![]() (m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)点B的坐标为 ,点D的坐标为 ;(用含有m的代数式表示)
(2)连接CD,BC.
①若![]() ,求二次函数的表达式;
,求二次函数的表达式;
②若把ABC沿着直线BC翻折,点A恰好在直线CD上,求二次函数的表达式.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)令![]() 解方程求出
解方程求出![]() 的值,结合点B的位置可得答案,由顶点的横坐标公式求得顶点横坐标,再代入解析式求解纵坐标即可.
的值,结合点B的位置可得答案,由顶点的横坐标公式求得顶点横坐标,再代入解析式求解纵坐标即可.
(2)①过点D作DH⊥AB,过点C作CG⊥DH,得到AB//CG,利用平行线的性质,锐角三角函数得![]() ,
,![]() 从而可求解函数解析式,
从而可求解函数解析式,
②过点B作BM⊥AC,BN⊥CD,由翻折得到角平分线,利用角平分线的性质得![]() ,利用三角形面积关系得到
,利用三角形面积关系得到![]() ,利用两点间距离公式列方程求解即可.
,利用两点间距离公式列方程求解即可.
解:(1)令![]()
![]()
![]()
![]()
![]() 点A在点B的左侧,
点A在点B的左侧,
![]()
![]()
![]() ,
,
![]() 抛物线的顶点横坐标为
抛物线的顶点横坐标为![]()
![]() 顶点纵坐标为:
顶点纵坐标为:![]()
![]() 顶点
顶点![]()
![]() .
.
故答案为: ![]() ,
,![]() .
.
(2)①过点D作DH⊥AB,过点C作CG⊥DH,
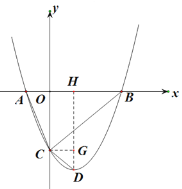
由题可知,C(0,﹣3m2),A(﹣m,0),B(3m,0),
∴![]() ,
,![]() ,
,
∵AB//CG
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
②过点B作BM⊥AC,BN⊥CD,
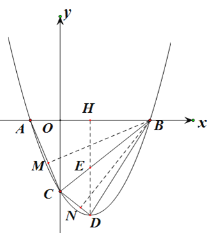
∵翻折
∴![]()
∵BM⊥AC,BN⊥CD,
∴![]()
由C(0,﹣3m2),A(﹣m,0),B(3m,0),D![]()
得![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40