题目内容
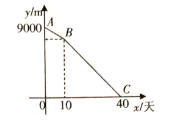
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中![]() 分别为线段,
分别为线段,![]() 为双曲线的一部分):
为双曲线的一部分):
(1)上课后第![]() 与第
与第![]() 相比较,何时学生注意力更集中?
相比较,何时学生注意力更集中?
(2)某道难题需连续讲![]() ,为保证效果,学生注意力指数不宜低于
,为保证效果,学生注意力指数不宜低于![]() ,老师能否在所需要求下讲完这道题?
,老师能否在所需要求下讲完这道题?
【答案】(1)上课后第![]() 的注意力更集中;(2)老师能在所需要求下讲完这道题,理由见详解.
的注意力更集中;(2)老师能在所需要求下讲完这道题,理由见详解.
【解析】
(1)先用待定系数法求出线段AB,CD的函数解析式,然后分别求出第![]() 与第
与第![]() 的注意力指数,然后进行比较即可;
的注意力指数,然后进行比较即可;
(2)分别求出注意力指数为36时的两个时间,然后再将时间差与19分钟进行比较,如果大于等于19则能讲完,否则不能.
(1)设线段AB的解析式为![]()
将![]() 代入解析式中得
代入解析式中得
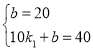 解得
解得![]()
∴线段AB解析式为![]() .
.
设线段CD的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]() ,
,
∴线段CD解析式为![]()
∵当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴上课后第![]() 的注意力更集中;
的注意力更集中;
(2)老师能在所需要求下讲完这道题,理由如下:
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]()
∵![]() ,
,
∴老师能在所需要求下讲完这道题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某校九年级(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
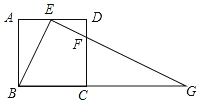
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为16,求BG的长.
【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.