题目内容
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1x2|≥|y1y2|,则点P1与点P2的“非常距离”为|x1x2|;
若|x1x2||y1y2|,则点P1与点P2的“非常距离”为|y1y2|.
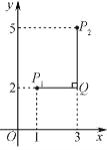
例如:点P1(1,2),点P2(3,5),因为|13||25|,所以点P1与点P2的“非常距离”为|25|3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
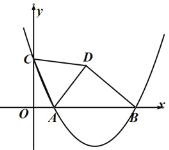
(1)已知点A(0,1),
①在B(![]() ,0),C(2,1),D(1,2),E(0,
,0),C(2,1),D(1,2),E(0,![]() )四个点中,与点A的“非常距离”为
)四个点中,与点A的“非常距离”为![]() 的点是;
的点是;
②点F为x轴上一动点,直接写出点A与点F的“非常距离”的最小值;
(2)已知点M是直线y2x6上的一个动点,
①点G的坐标是(0,2),求点M与点G的“非常距离”的最小值及相应的点M的坐标;
①点N是以点(4,0)为圆心,![]() 为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
【答案】(1)①B ,E;②1; (2)①点 M 的坐标为(![]() ),②M 与点 N 的“非常距离”的最小值为 3,M(1, 4).
),②M 与点 N 的“非常距离”的最小值为 3,M(1, 4).
【解析】
(1)①由“非常距离”的定义可以确定在B(![]() ,0),C(2,1),D(1,2),E(0,
,0),C(2,1),D(1,2),E(0,![]() )四个点中,与点A的“非常距离”,据此可以得答案;
)四个点中,与点A的“非常距离”,据此可以得答案;
②设点F的坐标为(x,0),根据|0-x|<|0-1|,得出点F与点A的“非常距离”最小值为|0-1|=1,即可得出答案;
(2)①设点M的坐标为(x0,2x06),先确定出M点的位置,由M在直线y=2x+6上,设出M点坐标(x0,2x06),由条件可求得M点坐标及点M与点G的“非常距离”d的最小值及相应的点M的坐标;;
②当点P在过原点且与直线y=-2x-6垂直的直线上时,点M与点P的“非常距离”最小,利用相似求出P(2,1),进而求解即可.
解:
(1)①根据定义可得:
点A(0,1)与点B(![]() ,0)的“非常距离”为
,0)的“非常距离”为![]() =
=![]() ;
;
点A(0,1)与点C(2,1)的“非常距离”为![]() =2;
=2;
点A(0,1)与点D(-1,2)的“非常距离”为![]() =1;
=1;
点A(0,1)与点E(0,-![]() )的“非常距离”为
)的“非常距离”为![]() =
=![]() ;
;
故与点A的“非常距离”为![]() 的是B,E.
的是B,E.
(2)设点F的坐标为(x,0),若点F与点A的“非常距离”最小值,则|0-x|<|0-1|故为“非常距离”最小值|0-1|=1,
故答案为①B,E;②1;
(2)①过M点作y轴的垂线,垂足为点H,连结MG,当点M在点G的左上方且使△MGH为等腰直角三角形时,点M与点G的“非常距离”最小.
设点M的坐标为(x0,2x06),由HM=HN得
|x0-0|=|2x06-2|,解得:x0=-4,或x0=![]()
∴点M的坐标为(-4,-2)或(![]() ,
,![]() ),
),
∴HM=HN=4或![]() ,
,
∴点M与点N的“非常距离”的最小值为![]() ,相应的M的坐标为(
,相应的M的坐标为(![]() ,
,![]() );
);
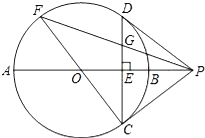
②.当点N在过圆心P且与直线y=2x+6垂直的直线上时,点M与点N的“非常距离”最小,设N(x,y)(点N位于第一象限).过N点作NH⊥x轴,
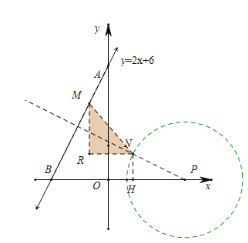
直线y=2x+6交坐标轴于A(0,6),B(-3,0),
∴AB=3![]() ,
,
∵△PBM∽△PNH,
∴![]()
∵PN=![]()
∴NH=1,PH=2,
∵P(4,0),
∴N(2,1),
当2-x02x061
∴x01
∴M(1,4),
点M与点N的“非常距离”的最小值为3.

【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
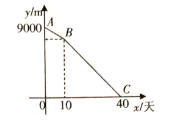
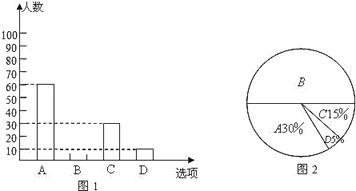
【题目】电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表:
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |

请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.