题目内容
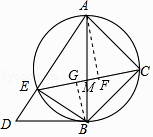
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC. 
(1)求证:EC平分∠AEB;
(2)求 ![]() 的值.
的值.
【答案】
(1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,
∴∠AEC=∠BEC,
即EC平分∠AEB
(2)解:如图,设AB与CE交于点M.
∵EC平分∠AEB,
∴ ![]() =
= ![]() .
.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE= ![]() =
= ![]() ,
,
∴AE= ![]() BE,
BE,
∴ ![]() =
= ![]() =
= ![]() .
.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,
∴△AFM∽△BGM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;(2)设AB与CE交于点M.根据角平分线的性质得出 ![]() =
= ![]() .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=
.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE= ![]() BE,那么
BE,那么 ![]() =
= ![]() =
= ![]() .作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出
.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出 ![]() =
= ![]() =
= ![]() ,进而求出
,进而求出 ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【考点精析】本题主要考查了圆周角定理和相似三角形的判定与性质的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |

(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.





