Question

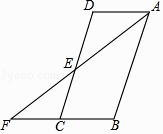
【题目】某课桌生产厂家研究发现，倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势．根据这一研究，厂家决定将水平桌面做成可调节角度的桌面．新桌面的设计图如图1所示，AB可绕点A旋转，在点C处安装一根可旋转的支撑臂CD，AC=30cm．

（1）如图2，当∠BAC=24°时，CD⊥AB，求支撑臂CD的长．

（2）如图3，当∠BAC=12°，求AD的长（结果保留根号）．
[参考数据：sin24°=0.40，cos24°=0.91，tan24°=0.46，sin12°=0.20]

Answer 1

【答案】
（1）

解：在Rt△ACD中，∵∠DAC=24°，∠ADC=90°，

∴sin24°= ，

∴CD=ACsin24°=30×0.40=12cm；

∴此时支撑臂CD的长为12cm

（2）

解：如图2，过点C作CE⊥AB于点E，

当∠BAC=12°时，

∴sin12°= = ，

∴CE=30×0.20=6cm，

∵CD=12cm，

∴DE= = =6 cm，

∴AE= =12 cm，

如图3有两种情况：

∴AD的长为（12 +6 ）cm或（12 ﹣6 ）cm．

【解析】（1）在Rt△ACD中利用锐角三角函数关系得出sin24°= ，代入数值计算即可求出CD的长；（2）过点C作CE⊥AB于点E，在Rt△ACE中利用锐角三角函数关系得出sin12°= ，求出CE的长，再根据勾股定理求出DE，AE的长，进而得出AD的长．