题目内容
【题目】如图，在平面直角坐标系中，抛物线y= 
x2经过平移得到抛物线y=ax2+bx，其对称轴与两段抛物线所围成的阴影部分的面积为 
，则a、b的值分别为（ ） 
A. ， 
B. ，﹣
C. ，﹣
D.﹣ ，
【答案】C
【解析】解：如图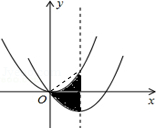 
，
∵y=ax2+bx= 
x2+bx= （x+ 
）2﹣ 
，
∴平移后抛物线的顶点坐标为（﹣ ，﹣ ），对称轴为直线x=﹣ ，
当x=﹣ 时，y= ，
∴平移后阴影部分的面积等于如图三角形的面积，
×（ + ）×（﹣ ）= 
．
解得b=﹣ 
，
故选：C．
【考点精析】掌握二次函数图象的平移是解答本题的根本，需要知道平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减．
练习册系列答案
相关题目
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛，在选拔赛中，每人射击10次，然后从他们的成绩平均数（环）及方差两个因素进行分析，甲、乙、丙的成绩分析如表所示，丁的成绩如图所示．
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
根据以上图表信息，参赛选手应选（ ）
A.甲
B.乙
C.丙
D.丁
