题目内容
【题目】根据阅读材料,回答问题.
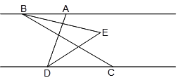
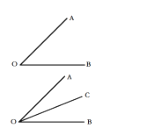
材料:如图所示,有公共端点(O)的两条射线组成的图形叫做角(![]() ).如果一条射线(
).如果一条射线(![]() )把一个角(
)把一个角(![]() )分成两个相等的角(
)分成两个相等的角(![]() 和
和![]() ),这条射线(
),这条射线(![]() )叫做这个角的平分线.这时,
)叫做这个角的平分线.这时,![]() (或
(或![]() ).
).
问题:平面内一定点A在直线![]() 的上方,点O为直线
的上方,点O为直线![]() 上一动点,作射线
上一动点,作射线![]() ,
,![]() ,
,![]() ,当点O在直线
,当点O在直线![]() 上运动时,始终保持
上运动时,始终保持![]() ,
,![]() ,将射线
,将射线![]() 绕点O顺时针旋转60°得到射线
绕点O顺时针旋转60°得到射线![]() .
.
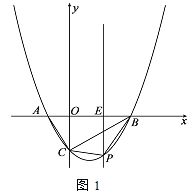
(1)如图1,当点O运动到使点A在射线![]() 的左侧时,若
的左侧时,若![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
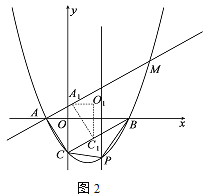
(2)当点O运动到使点A在射线![]() 的左侧,
的左侧,![]() 时,求
时,求![]() 的值;
的值;
(3)当点O运动到某一时刻时,![]() ,直接写出此时
,直接写出此时![]() 的度数.
的度数.

【答案】(1)40°;(2)![]() 或
或![]() (3)105°或135°.
(3)105°或135°.
【解析】
(1)根据角的平分线定义及角的和差即可求解;
(2)当射线OB在∠A′OP内部和外部两种情况进行讨论求解;
(3)分两种情况讨论如图4和图5进行推理即可.
解:(1)设![]() 的度数为x.
的度数为x.
由题意知:![]() ,
,![]() ;
;
因为![]() 平分
平分![]() ,所以
,所以![]() ;
;
所以![]() ;
;
解得,![]() ;
;
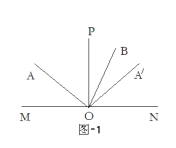
(2)①如图-2-1,当射线![]() 在
在![]() 内部时:设
内部时:设![]() 的度数为y.
的度数为y.
由题意可知:![]() ,
,![]() ;
;
因为![]() ,所以
,所以![]() ;
;
因为![]() ,所以
,所以![]() ;
;
因为![]() ;
;
所以![]() ;
;
解得,![]() .
.

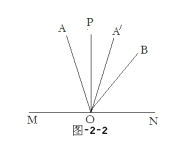
②如图-2-2,当射线![]() 在
在![]() 外部时:设
外部时:设![]() 的度数为y.
的度数为y.
由题意可知:![]() ,
,![]() ;
;
因为![]() ,所以
,所以![]() ;
;
因为![]() ,所以
,所以![]() ;
;
因为![]() ;
;
所以![]() ;
;
解得,![]() .
.
(3)105°或135°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目