题目内容
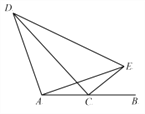
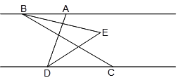
【题目】如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E.∠ADC =68°.
（1）求∠EDC的度数；
（2）若∠ABC =n°，求∠BED的度数（用含n的代数式表示）；
（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED的度数是否改变，若改变，求出它的度数（用含n的式子表示），不改变，请说明理由.
【答案】（1）34°；（2）
n°+34°；（3）图形见解析；发生了改变， （214－n）°.
【解析】
（1）根据角平分线的定义即可求∠EDC的度数；
（2）过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；
（3）∠BED的度数改变．过点E作EF∥AB，先由角平分线的定义可得：
，然后根据两直线平行内错角相等及同旁内角互补可得：
进而可求
解：（1）∵DE平分∠ADC，∠ADC=68°，
∴
（2）过点E作EF∥AB，
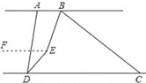
∵AB∥CD，
∴AB∥CD∥EF，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=68°，
∴
∴
（3）过点E作EF∥AB
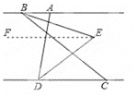
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=68°
∴
∵AB∥CD，
∴AB∥CD∥EF，
∴
∴
故∠BED的度数发生了改变，改变为
练习册系列答案
相关题目
