题目内容
【题目】在梯形ABCD中,AD∥BC,AB=CD=AD=5cm,BC=11cm,点P从点D开始沿DA边以每秒1cm的速度移动,点Q从点B开始沿BC边以每秒2cm的速度移动(当点P到达点A时,点P与点Q同时停止移动),假设点P移动的时间为x(秒),四边形ABQP的面积为y(cm2).
(1)求y关于x函数解析式,并写出它的定义域;
(2)在移动的过程中,PQ是否可能平分对角线AC?若能,求出x的值;若不能,请说明理由;
(3)在移动的过程中,是否从在x使得PQ=AB,若存在求出所有x的值,若不存在请说明理由.

【答案】(1)2x+10,(0≤x≤5);(2)能,x=3;(3)存在,当x=![]() 或x=
或x=![]() 时,PQ=AB
时,PQ=AB
【解析】
(1)根据题意求出梯形的高,根据梯形的面积公式写出y关于x的函数解析式和定义域;
(2)四边形ABQP的面积与四边形QCDP的面积相等时,四边形ABQP的面积=四边形ABCD的面积的一半列出算式解答即可;
(3)根据平行四边形的性质和等腰梯形的性质解答即可.
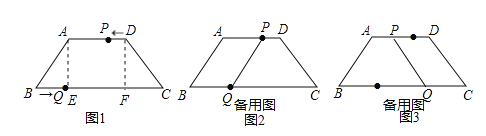
(1)如图1,作AE⊥BC于E,DF⊥BC与F,
∵AB=CD=AD=5cm,BC=11cm,
∴BQ=CF=3,
由勾股定理得,AE=4,
则y=![]() ×(5-x+2x)×4=2x+10,(0≤x≤5);
×(5-x+2x)×4=2x+10,(0≤x≤5);
(2)四边形ABQP的面积与四边形QCDP的面积相等时,
四边形ABQP的面积=四边形ABCD的面积的一半,
即2x+10=![]() ×
×![]() (5+11)×4,
(5+11)×4,
解得,x=3;
(3)如图2,当四边形ABQP为平行四边形时,PQ=AB,
即AP=BQ,此时,5-x=2x,
解得,x=![]() ,
,
如图3,当四边形ABQP为等腰梯形时,PQ=AB,
此时四边形PQCD是平行四边形,
x=11-2x,
解得,x=![]() ,
,
∴当x=![]() 或x=
或x=![]() 时,PQ=AB.
时,PQ=AB.

 阅读快车系列答案
阅读快车系列答案【题目】今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。”卖菜阿姨说:“下雪天从地里弄菜不容易啊,所以你花这些钱要比昨天少买1斤了。”王大爷回答道:“应该的,你们也真的辛苦。”
青菜 | 花菜 | 大白菜 | |
1月24日 | 2元/斤 | 5元/斤 | 1元/斤 |
1月25日 | 2.5元/斤 | 7元/斤 | 1.5元/斤 |
(1)请问超市三种蔬菜中哪种涨幅最大?并计算其涨幅;
(2)请你根据王大爷和卖菜阿姨的对话,来算算,这天王大爷买了几斤菠菜?