题目内容
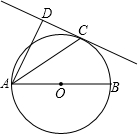
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2.求CD的长.

(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2.求CD的长.

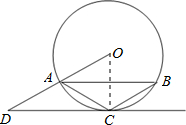
(1)CD与⊙O相切.理由如下:
如图,连接OC,
∵CA=CB,
∴
=
∴OC⊥AB,
∵CD∥AB,
∴OC⊥CD,
∵OC是半径,
∴CD与⊙O相切.
(2)∵CA=CB,∠ACB=120°,
∴∠ABC=30°,
∴∠DOC=60°
∴∠D=30°,
∵OA=OC=2,
∴D0=4,
∴CD=
=2
如图,连接OC,
∵CA=CB,
∴
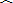 |
| AC |
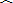 |
| CB |
∴OC⊥AB,
∵CD∥AB,
∴OC⊥CD,
∵OC是半径,
∴CD与⊙O相切.
(2)∵CA=CB,∠ACB=120°,
∴∠ABC=30°,
∴∠DOC=60°
∴∠D=30°,
∵OA=OC=2,
∴D0=4,
∴CD=
| DO2-OC2 |
| 3 |


练习册系列答案
相关题目