题目内容
如图,已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,AD⊥PC于D,CE⊥AB于E,求证:
(1)AD=AE
(2)PC•CE=PA•BE.

(1)AD=AE
(2)PC•CE=PA•BE.

证明:(1)连AC、BC,OC,如图,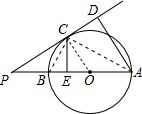
∵PC是⊙O的切线,
∴OC⊥PD,
而AD⊥PC,
∴OC∥PD,
∴∠ACO=∠CAD,
而∠ACO=∠OAC,
∴∠DAC=∠CAO,
又∵CE⊥AB,
∴∠AEC=90°,
∴Rt△ACE≌Rt△ACD,
∴CD=CE,AD=AE;
(2)在Rt△PCE和Rt△PAD中,∠CPE=∠APD,
∴Rt△PCE∽Rt△PAD,
∴PC:PA=CE:AD,
又∵AB为⊙O的直径,
∴∠ACB=90°,
而∠DAC=∠CAO,
∴Rt△EBC∽Rt△DCA,
∴BE:CE=CD:AD,
而CD=CE,
∴BE:CE=CE:AD,
∴BE:CE=PC:PA,
∴PC•CE=PA•BE.

∵PC是⊙O的切线,
∴OC⊥PD,
而AD⊥PC,
∴OC∥PD,
∴∠ACO=∠CAD,
而∠ACO=∠OAC,
∴∠DAC=∠CAO,
又∵CE⊥AB,
∴∠AEC=90°,
∴Rt△ACE≌Rt△ACD,
∴CD=CE,AD=AE;
(2)在Rt△PCE和Rt△PAD中,∠CPE=∠APD,
∴Rt△PCE∽Rt△PAD,
∴PC:PA=CE:AD,
又∵AB为⊙O的直径,
∴∠ACB=90°,
而∠DAC=∠CAO,
∴Rt△EBC∽Rt△DCA,
∴BE:CE=CD:AD,
而CD=CE,
∴BE:CE=CE:AD,
∴BE:CE=PC:PA,
∴PC•CE=PA•BE.

练习册系列答案
相关题目







 于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.