Question

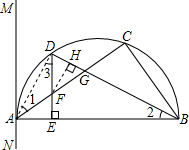
如图，△ABC内接于半圆，AB为直径，过点A作直线MN，若∠MAC=∠ABC．
（1）求证：MN是半圆的切线．
（2）设D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F，求证：FD=FG．
（3）在（2）的条件下，若△DFG的面积为4.5，且DG=3，GC=4，试求△BCG的面积．

Answer 1

（1）证明：∵AB是直径，
∴∠ACB=90°．
∴∠CAB+∠ABC=90°．（1分）
∵∠MAC=∠ABC，
∴∠MAC+∠CAB=90°．
即MA⊥AB．
∴MN是半圆的切线．（2分）

（2）证明：
证法1：∵D是弧AC的中点，
∴∠DBC=∠2．（3分）
∵AB是直径，
∴∠CBG+∠CGB=90°．
∵DE⊥AB，
∴∠FDG+∠2=90°．（4分）
∵∠DBC=∠2，
∴∠FDG=∠CGB=∠FGD．
∴FD=FG．（5分）
证法2：连接AD，则∠1=∠2，（3分）
∵AB是直径，
∴∠ADB=90°．
∴∠1+∠DGF=90°．
又∵DE⊥AB，
∴∠2+∠FDG=90°．（4分）
∴∠FDG=∠FGD．
∴FD=FG．（5分）

（3）解法1：过点F作FH⊥DG于H，（6分）
又∵DF=FG，
∴S_△FGH=

1

2

S_△DFG=

1

2

×4.5=

9

4

．（7分）
∵AB是直径，FH⊥DG，
∴∠C=∠FHG=90°．（8分）
∵∠HGF=∠CGB，
∴△FGH∽△BGC．
∴

S△FGH

S△BGC

=(

HG

CG

)2=(

1.5

4

)2=

9

64

．（9分）
∴S_△BCG=

9

4

×

64

9

=16．（10分）

解法2：∵∠ADB=90°，DE⊥AB，
∴∠3=∠2．（6分）
∵∠1=∠2，
∴∠1=∠3．
∴AF=DF=FG．（7分）
∴S_△ADG=9．（8分）
∵∠ADG=∠BCG，∠DGA=∠CGB．
∴△ADG∽△BCG．（9分）
∴

S△BCG

S△ADG

=(

CG

DG

)2=(

4

3

)2=

16

9

．
∴S_△BCG=

16

9

×9=16．（10分）

解法3：连接AD，过点F作FH⊥DG于H．
∵S_FDG=

1

2

DG×FH=

1

2

×3FH=4.5，
∴FH=3．
∵H是DG的中点，FH∥AD，
∴AD=2FH=6
∴S_△ADG=

1

2

AD•DG=

1

2

×6×3=9．
∵∠ADG=∠BCG，∠DGA=∠CGB．
∴△ADG∽△BCG．
∵DG=3，GC=4，
∴

S△ADG

S△BCG

=（

DG

CG

）²，
∴

9

S△BCG

=（

3

4

）²，
∴S_△BCG=16．