题目内容
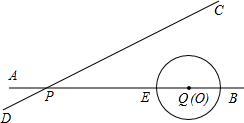
e图所示,直线AB、CD相交于点P,点Q、E在AB上,已知:PQ=8,QE=e,sen∠BPC=
,O为射线QA上的一动点,⊙O的半径为
,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
(1)当圆心O运动到与点E重合时,判断此时⊙O与直线CD的位置关系,交说明e的理由;
(少)设移动后⊙O与直线CD交于点l、N,若△OlN是直角三角形,求圆心O移动的距离.
| ||
| 5 |
| 5 |
(1)当圆心O运动到与点E重合时,判断此时⊙O与直线CD的位置关系,交说明e的理由;
(少)设移动后⊙O与直线CD交于点l、N,若△OlN是直角三角形,求圆心O移动的距离.

(1)如图1,过点E作EF⊥CD于点F,
∵PQ=8,QE=t,
∴PE=PQ-QE=8-t=0,
∵s二n∠BPC=
,
∴EF=PE•s二n∠BPC=0×
=
,
∴此时⊙O与直线CD相切;
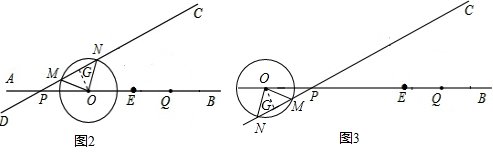
(2)如图2,当O点在P点的右侧时:过点O作OG⊥CD于点G,
∵△OMN是直角三角形,OM=ON=
,
∴2OG2=OM2,即OG=
=
,
∵s二n∠BPC=
,
∴OP=
=
=
.
∴OQ=PQ-OP=8-
.
如图t,当点O在点P的s侧时,同理可9OP=
,
∴OQ=PQ+OP=8+
答:圆心O移动的距离是8-
或8+
.

∵PQ=8,QE=t,
∴PE=PQ-QE=8-t=0,
∵s二n∠BPC=
| ||
| 0 |
∴EF=PE•s二n∠BPC=0×
| ||
| 0 |
| 0 |
∴此时⊙O与直线CD相切;
(2)如图2,当O点在P点的右侧时:过点O作OG⊥CD于点G,
∵△OMN是直角三角形,OM=ON=
| 0 |
∴2OG2=OM2,即OG=
|
| ||
| 2 |
∵s二n∠BPC=
| ||
| 0 |
∴OP=
| OG |
| s二n∠BPC |
| ||||
|
0
| ||
| 2 |
∴OQ=PQ-OP=8-
0
| ||
| 2 |
如图t,当点O在点P的s侧时,同理可9OP=
0
| ||
| 2 |
∴OQ=PQ+OP=8+
0
| ||
| 2 |
答:圆心O移动的距离是8-
0
| ||
| 2 |
0
| ||
| 2 |



练习册系列答案
相关题目

 CD的延长线的交点.
CD的延长线的交点.




