Question

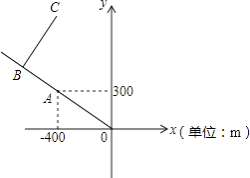
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步，先到终点的人原地休息．已知甲先出发3秒，在跑步过程中，甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示，则下列结论正确的个数有（ ）

①乙的速度是4米／秒；
②离开起点后，甲、乙两人第一次相遇时，距离起点12米；
③甲从起点到终点共用时83秒；
④乙到达终点时，甲、乙两人相距68米；
⑤乙离开起点12秒后，甲乙第一次相遇．
A.4个
B.3个’
C.2个
D.1个

Answer 1

【答案】C
【解析】解 :由函数图象，得：甲的速度为12÷3=4米/秒，乙的速度为400÷80=5米/秒，故①不符合题意；
设乙离开起点x秒后，甲、乙两人第一次相遇，根据题意得：
5x=12+4x，
解得：x=12，
∴离开起点后,甲、乙两人第一次相遇时,距离起点为：12×5=60(米)，故②不符合题意，故⑤符合题意；
甲从起点到终点共用时为：400÷4=100(秒)，故③不符合题意；
∵乙到达终点时，所用时间为80秒，甲先出发3秒，
∴此时甲行走的时间为83秒，
∴甲走的路程为：83×4=332(米)，
∴乙到达终点时,甲、乙两人相距：400332=68(米)，故④符合题意；
故答案为：C .
通过函数图象可得，甲出发3秒走的路程为12米，乙到达终点所用的时间为80秒，根据行程问题的数量关系可以求出甲、乙的速度，利用数形结合思想及一元一次方程即可求出甲乙第一次相遇时，乙出发的时间，乙到达终点时甲离终点的距离，及甲行完全程所用的时间，从而能做出判断得出答案。