题目内容
【题目】如图,直线AB:y=一 ![]() x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ![]() ),与直线AB交于点E.
),与直线AB交于点E.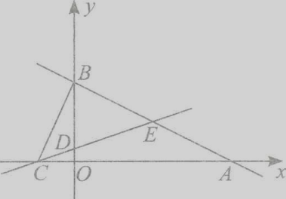
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
【答案】
(1)解:设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: 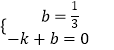
∴ ![]()
∴直线 ![]() 表达式为:
表达式为: ![]()
(2)解:∵ 
∴ ![]() , ∴E(2,1),
, ∴E(2,1),
∵C(-1,0),A(4,0),
∴A C=5, OB=2, ![]()
∴ ![]()
![]()
![]()
![]()
(3)解:点 ![]() 关于直线
关于直线 ![]() 的对称点为
的对称点为 ![]() ,连接
,连接 ![]() 交直线
交直线 ![]() 于点
于点 ![]() ,则点
,则点 ![]() 即为所求的点
即为所求的点

设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: ![]()
∴ ![]()
∴ ![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]() ∴
∴ ![]()
∴m= ![]()
【解析】(1)设直线 C D 表达式为: y = k x + b,用待定系数法即可求出直线CD的解析式 ;
(2)首先解直线AB与直线CD的解析式联立的方程组求出E点的坐标,根据A,B,C,E四点的坐标得出AC,OB的长,及E点到y轴的距离,根据 S Δ B C E = S Δ A B C S Δ A C E带值计算即可;
(3) E 关于直线 y = 2 的对称点为 E’ ( 2 , 3 ) ,连接 A E’交直线 y = 2 于点 Q ,则点 Q 即为所求的点,用待定系数法求出直线 A E’的解析式,然后把y=2代入直线 A E’的解析式求出对应的x的值,从而得出Q点的坐标,得到m的值。

【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.