Question

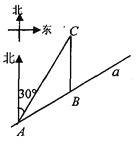
【题目】如图，某市郊外景区内一条笔直的公路a经过A、B两个景点，景区管委会又开发了风景优美的景点C，经测量景点C位于景点A的北偏东30°方向8km处，位于景点B的正北方向，已知AB＝5km．

(1)求景点B与景点为C的距离；（结果保留根号）

(2)为方便游客到景点游玩，景区管委会准备由景点C向公路a修建一条距离最短的公路，不考虑其它因素，求出这条公路的长．（结果精确到0.1km.参考数据： ＝1.73， ＝2.24）

Answer 1

【答案】（1）景点B与景点为C的距离为(3)km；（2）这条公路长约为3.1km.

【解析】试题分析：（1）过点A作AD⊥CB，交CB的延长线于点D，先解Rt△ADC，得出CD=4，再解Rt△ABD，得出BD=3，则BC=CD-BD；（2）过点C作CE⊥AB于点E．在Rt△CBE中，由正弦函数的定义即可求解．

试题解析：（1）如图，过点A作AD⊥CB，交CB的延长线于点D.

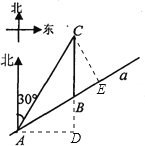
在Rt△ADC中，∠ADC=90°，∠ACD=30°，

∴AD=AC=×8=4，

∴CD=.

在Rt△ABD中,BD=，

∴BC=CDBD=3，

答：景点B与景点为C的距离为(3)km；

(2)过点C作CE⊥AB于点E.sin∠ABD=.

在Rt△CBE中,sin∠CBE=，

∵∠ABD=∠CBE，

∴sin∠CBE=，

∴CE=CBsin∠CBE=(3)×=≈3.1(km).

答：这条公路长约为3.1km.