题目内容
【题目】如图是根据宝塔山公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(﹣400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向右转90°后直行400m到达樱花园C,则点C的坐标是 . 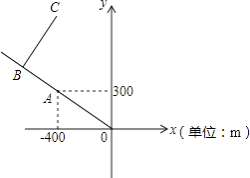
【答案】(﹣400,800)
【解析】解:连接AC, 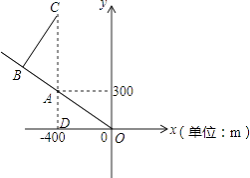
由题意可得:AB=300m,BC=400m,
在△AOD和△ACB中
∵ 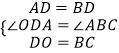 ,
,
∴△AOD≌△ACB(SAS),
∴∠CAB=∠OAD,
∵B、O在一条直线上,
∴C,A,D也在一条直线上,
∴AC=AO=500m,则CD=AC+AD=800m,
∴C点坐标为:(﹣400,800).
所以答案是:(﹣400,800).
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目