题目内容
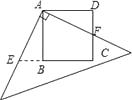
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.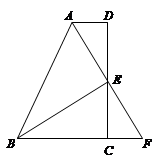
求证:
(1)AD=FC;
(2)AB=BC+AD
【答案】
(1)证明:∵AD∥BC,
∴![]() ADC=
ADC=![]() ECF,
ECF,
∵E是CD的中点,
∴DE=EC,
在![]() ADE和
ADE和![]() FCE中,
FCE中, ,
,
∴![]() ADE
ADE![]()
![]() FCE(ASA),
FCE(ASA),
∴AD=FC.
(2)证明:∵![]() ADE
ADE![]()
![]() FCE,
FCE,
∴AE=EF,AD=CF,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF,
∴AB=BC+AD.
【解析】(1)根据AD∥BC可知![]() ADC=
ADC=![]() ECF,再根据E是CD的中点可证出
ECF,再根据E是CD的中点可证出![]() ADE
ADE![]()
![]() FCE,进而根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
FCE,进而根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.