Question

【题目】如图所示，在△ABC中， C=2 B，点D是BC上一点，AD=6，且AD AB，点E是BD上的点，AE= BD，AC=5，贝AB的长度为 ．

Answer 1

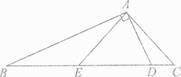
【答案】8
【解析】解：∵AD⊥AB ,
∴△ABD为直角三角形。
又∵点E是BD的点，且AE= BD
∴点E是BD上的中点，
∴BE=DE=AE ,
∴∠EAB=∠B ,
∴∠AEC=∠B+∠EAB=2∠B=∠C，即∠AEC=∠C，
∴AE=AC=5.
在Rt△ABD中，AD=6，BD=2AE=2×5=10 ;
∴AB=8 .
故答案为 ：8 。

在Rt△ADB中，点E是BD的点及AE= BD；根据直角三角形的性质，可得BE=AE，根据等边对等角得出∠AEC=2∠B=∠C，根据等角对等边得出则AE=AC；从而得出BD的长 ，根据勾股定理可得AB的长度 。