Question

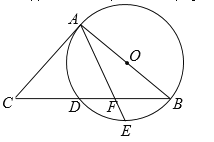
【题目】如图，AB是⊙O的直径， BC交⊙O于点D，E是的中点，连接AE交BC于点F，∠ACB =2∠EAB．

（1）判断直线AC与⊙O的位置关系，并说明理由；

（2）若，，求BF的长．

Answer 1

【答案】（1）AC是⊙O的切线，见解析；（2）

【解析】

（1）首先证明∠ACB =∠BAD，然后根据圆周角定理的推论得出∠ACB +∠CAD=90°，则有∠BAD+∠CAD=90°，所以BA⊥AC，则可证明AC是⊙O的切线；

（2）过点F做FH⊥AB于点H．首先通过角平分线的性质得出FH=FD，且FH∥AC，然后利用锐角三角函数求出CD,BD的长度，然后设 DF=x，则FH=x，，最后利用建立关于x的方程，解方程即可得出答案．

解：（1）AC是⊙O的切线

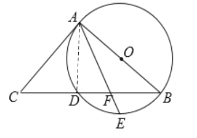
理由:如图，连接AD．

∵ E是中点，

∴．

∴ ∠DAE=∠EAB．

∵ ∠ACB =2∠EAB，

∴∠ACB =∠BAD．

∵ AB是⊙O的直径，

∴ ∠ADB=∠ADC=90°，

∴ ∠ACB +∠CAD=90°，

∴ ∠BAD+∠CAD=90°．

即 BA⊥AC．

∴ AC是⊙O的切线．

（2）解：如图，过点F做FH⊥AB于点H．

∵ AD⊥BD，FH⊥AB，∠DAE=∠EAB，

∴ FH=FD，且FH∥AC．

在Rt△ADC中，

∵，，

∴ CD=6．

同理，在Rt△BAC中，可求得．

∴．

设 DF=x，则FH=x，．

∵ FH∥AC，

∴ ∠BFH=∠ACB．

∴．

即．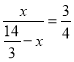

解得x=2，

经检验，x=2是原分式方程的解，

∴．