题目内容
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论:![]() ;
;![]() >0;(3)若点
>0;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
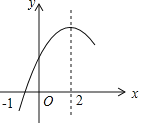
【答案】(1)(2)(4)
【解析】
根据二次函数的性质分别判断:(1)根据对称轴公式计算即可;(2)由图象可知抛物线经过(-1,0)和(5,0),列出方程组求出a、b即可判断;(3)利用函数图象即可判断;(4)利用二次函数与二次不等式关系即可解决问题.
∵![]() ,
,
![]() ,故(1)正确;
,故(1)正确;
∵抛物线与x轴的一个交点为![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,
,
∵抛物线开口向下,
![]() ,
,
![]() ,故(2)正确,
,故(2)正确,
∵抛物线的对称轴为![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,在对称轴的左侧,
,在对称轴的左侧,
![]() 随x的增大而增大,
随x的增大而增大,
![]() ,故(3)错误;
,故(3)错误;
方程![]() 的两根为
的两根为![]() 、
、![]() ,
,
过![]() 作x轴的平行线,直线
作x轴的平行线,直线![]() 与抛物线的交点的横坐标为方程的两根,
与抛物线的交点的横坐标为方程的两根,
依据函数图象可知:![]() ,故(4)正确,
,故(4)正确,
故答案为:(1)(2)(4).

【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
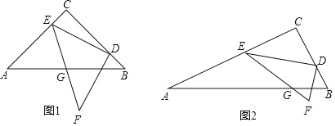
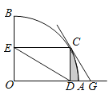
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.