Question

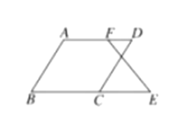
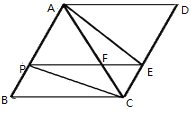
【题目】如图，在四边形ABCD中，，，连接AC，点P、E分别在AB、CD上，连接PE，PE与AC交于点F，连接PC，，．

（1）判断四边形PBCE的形状，并说明理由；

（2）求证：；

（3）当P为AB的中点时，四边形APCE是什么特殊四边形？请说明理由．

Answer 1

【答案】（1）四边形PBCE为平行四边形，证明过程见解析；（2）见解析；（3）四边形APCE为矩形，证明过程见解析.

【解析】

（1）证明四边形ABCD为平行四边形，从而得BP//CE，根据内错角相等证明AD//PE,从而可证PE//BC，得四边形PBCE为平行四边形；（2）证明△CBP≌△ACE即可证明CP=AE；（3）证明四边形APCE为平行四边形，然后根据三线合一证明∠APC=90°，可证四边形APCE为矩形.

解：（1）四边形PBCE为平行四边形.

证明：∵，，

∴四边形ABCD为平行四边形，

∴PB//EC,

∵,

∴AD//PE,

∴PE//BC,

∴四边形PBCE为平行四边形.

（2）∵四边形ABCD为平行四边形，

∴∠B=∠D，AB//CD,

∴

又∵，

∴∠B=，

∴BC=AC，

∵四边形PBCE为平行四边形，

∴PB=CE，

在△CBP和△ACE中

∴△CBP≌△ACE.

∴.

（3）四边形APCE为矩形，

证明：∵P为AB的中点

∴BP=AP,

∵四边形PBCE为平行四边形，

∴BP=CE,

∴AP=CE,

又∵AB//CD

∴四边形APCE为平行四边形，

∵CB=CA，AP=BP，

∴CP⊥AB，

∴∠APC=90°，

∴为矩形.