题目内容
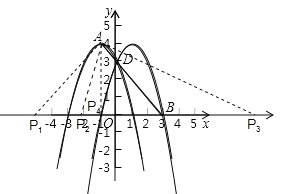
【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣
;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0).
,0)或(﹣1,0).
【解析】
试题分析:(1)设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 即可得到结论;
即可得到结论;
(2)解方程组得到![]() ,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
(3)根据轴对称的性质得到抛物线c2的解析式为:![]() ,根据图象即可刚刚结论;
,根据图象即可刚刚结论;
(4)求得B(3,0),得到OB=3,根据勾股定理得到AB的长,①当AP=AB,②当AB=BP=![]() 时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
试题解析:(1)∵抛物线c1的顶点为A(﹣1,4),∴设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:
得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:![]() ,即
,即![]() ;
;
(2)解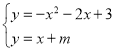 得
得![]() ,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=
,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=![]() ;
;
(3)∵抛物线c1关于y轴对称的抛物线记作c2,∴抛物线c2的顶点坐标为(1,4),与y轴的交点为(0,3),∴抛物线c2的解析式为:![]() ,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
②当直线l2过D(0,3)时,即n=3时,l2与c1和c2共有三个交点;
③当3<n<4或n<3时,l2与c1和c2共有四个交点;
(4)如图,∵若c2与x轴正半轴交于B,∴B(3,0),∴OB=3,∴AB=![]() =
=![]() :
:
①当AP=AB=![]() 时,PB=8,∴P1(﹣5,0);
时,PB=8,∴P1(﹣5,0);
②当AB=BP=![]() 时,P2(3﹣
时,P2(3﹣![]() ,0)或P3(3+
,0)或P3(3+![]() ,0);
,0);
③当AP=PB时,点P在AB的垂直平分线上,∴PA=PB=4,∴P4(﹣1,0).
综上所述,点P的坐标为(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0)时,△PAB为等腰三角形.
,0)或(﹣1,0)时,△PAB为等腰三角形.

 智慧小复习系列答案
智慧小复习系列答案