题目内容
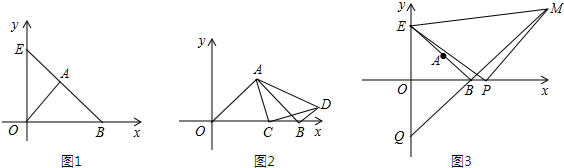
如图,直线BE交x轴正半轴于点B(a,0),交y轴正半轴于点E(0,b),且a、b满足
+|4-b|=0,点A为BE的中点,
(1)写出A点坐标为______;
(2)如图,若C为线段OB上一点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连BD,求证:OA∥BD;
(3)如图,P为x轴上B点右侧任意一点,以EP为边作等腰Rt△EPM,其中PE=PM,直线MB交y轴点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变;求其值;若变化,求线段OQ的取值范围.
| a-4 |
(1)写出A点坐标为______;
(2)如图,若C为线段OB上一点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连BD,求证:OA∥BD;
(3)如图,P为x轴上B点右侧任意一点,以EP为边作等腰Rt△EPM,其中PE=PM,直线MB交y轴点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变;求其值;若变化,求线段OQ的取值范围.

(1)∵
+
=0
∴a=4,b=4,
∴△EOB为等腰直角三角形.
∴点A的坐标为(2,2),
故答案为(2,2);
(2)∵以AC为直角边作等腰直角△ACD,∠ACD=90°,
∴∠CAB+∠BAD=45°,∠CDB+∠BAD+∠ADC=90°,
∴∠CAB=∠CDB,
∴∠ABD=90°=∠OAB,
∴OA∥BD;
(3)过M作MD⊥x轴,垂足为D.
∵∠EPM=90°,
∴∠EPO+MPD=90°.
∵∠QOB=∠MDP=90°,
∴∠EPO=∠PMD,∠PEO=∠MPD.
在△PEO和△MPD中,
∴△PEO≌△MPD,
MD=OP,PD=AO=BO,
OP=OA+AP=PD+AP=AD,
∴MD=AD,∠MAD=45°.
∵∠BAO=45°,
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴无论P点怎么动OQ的长不变.
| a-4 |
| . |
| . |
∴a=4,b=4,
∴△EOB为等腰直角三角形.
∴点A的坐标为(2,2),
故答案为(2,2);
(2)∵以AC为直角边作等腰直角△ACD,∠ACD=90°,
∴∠CAB+∠BAD=45°,∠CDB+∠BAD+∠ADC=90°,
∴∠CAB=∠CDB,
∴∠ABD=90°=∠OAB,

∴OA∥BD;
(3)过M作MD⊥x轴,垂足为D.
∵∠EPM=90°,
∴∠EPO+MPD=90°.
∵∠QOB=∠MDP=90°,
∴∠EPO=∠PMD,∠PEO=∠MPD.
在△PEO和△MPD中,
|
∴△PEO≌△MPD,
MD=OP,PD=AO=BO,
OP=OA+AP=PD+AP=AD,
∴MD=AD,∠MAD=45°.
∵∠BAO=45°,
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴无论P点怎么动OQ的长不变.

练习册系列答案
相关题目
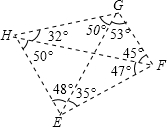

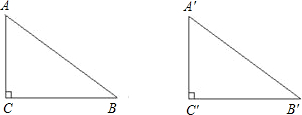 列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )
列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )