题目内容
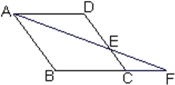
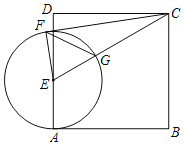
【题目】如图，四边形ABCD是正方形，E是AD边上的一个动点（有与A、D重合），以E为圆心，EA为半径的⊙E交CE于G点，CF与⊙E切于F点．AD＝4，AE＝x，CF2＝y．
（1）求y与x的函数关系式，并写出x的取值范围；
（2）是否存在x的值，使得FG把△CEF的面积分成1：2两部分？若存在，求出x的值；若不存在，请说明理由．
【答案】（1）y＝（4﹣x）2+16﹣x2＝32﹣8x（0＜x＜4）；（2）x＝
，或x＝
．
【解析】
（1）由已知EF⊥CF，再由正方形的性质可得CD＝AD＝4，∠ADC＝90°，根据勾股定理可求解；
（2）由同底等高类的数量关系，可得EG＝
EC，或EG＝
EC，可列出方程，即可求解．
解：（1）∵CF与⊙E切于F点，
∴EF⊥CF，
∵AE＝x，AD＝4，
∴DE＝4﹣x，
∵四边形ABCD是正方形，
∴CD＝AD＝4，∠ADC＝90°，
∴CE2＝DE2+CD2＝（4﹣x）2+16，
在Rt△EFC中，CF2＝CE2﹣EF2，
∴y＝（4﹣x）2+16﹣x2＝32﹣8x（0＜x＜4）；
（2）∵FG把△CEF的面积分成1：2两部分，
∴EG＝EC，或EG＝EC，
∴x＝
，或x＝
∴x＝±
，或x＝
∵0＜x＜4，
∴x＝，或x＝．
练习册系列答案
口算题天天练系列答案
相关题目
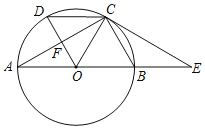
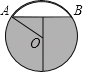
【题目】往水平放置的圆柱形油槽内装入一些油后，截面如图所示．若油面宽AB和油的最大深度都为80cm．
（1）求油槽的半径OA；
（2）从油槽中放出一部分油，当剩下的油面宽度为60cm时，求油面下降的高度．
【题目】已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣8 | ﹣3 | 0 | 1 | 0 | ﹣3 | … |
若A（m，y1），B（m﹣1，y2）两点都在该函数的图象上，当m满足范围_____时，y1＜y2．
