题目内容
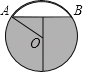
【题目】往水平放置的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB和油的最大深度都为80cm.
(1)求油槽的半径OA;
(2)从油槽中放出一部分油,当剩下的油面宽度为60cm时,求油面下降的高度.
【答案】(1)50cm,(2)70cm.
【解析】
(1)过O作OC⊥AB,延长CO与圆交于D,利用垂径定理得到AC的长度,设OA为xcm,然后在Rt△OAC中利用勾股定理建立方程求解;
(2)当油面下降到EF位置时,作出图形,连接OF,设CD与EF交于点G,在Rt△OGF中,利用勾股定理求出OG,则下降高度为OC+OG.
解:(1)如图,过O作OC⊥AB,延长CO与圆交于D,
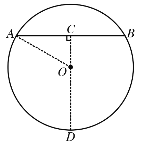
由题意可知AB=CD=80cm,
由垂径定理可得AC=CB=![]() AB=40cm,
AB=40cm,
设OA为xcm,则OC=(80-x)cm,
在Rt△OAC中,根据勾股定理可得:![]() ,
,
解得:x=50,
答:油槽的半径OA为50cm.
(2)如图,当油面下降到EF位置时,
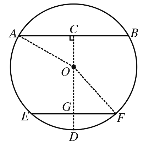
∵EF∥AB,CD⊥AB,
∴CD⊥EF,
连接OF,设CD与EF交于点G,由题意知EF=60cm,
由垂径定理可得GF=![]() EF=30cm,
EF=30cm,
在Rt△OGF中,![]()
由(1)可知OC=80-50=30cm
∴CG=OC+OG=30+40=70cm
答:油面下降的高度为70cm.

练习册系列答案
相关题目