题目内容
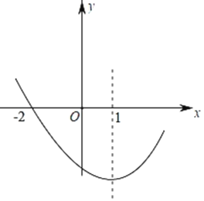
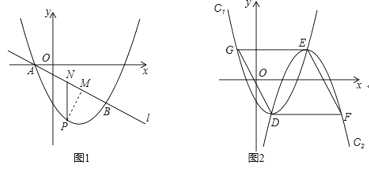
【题目】如图1,抛物线![]() :
:![]() 与直线l:
与直线l:![]() 交于x轴上的一点A,和另一点
交于x轴上的一点A,和另一点![]()
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
![]() 点P是抛物线
点P是抛物线![]() 上的一个动点
上的一个动点![]() 点P在A,B两点之间,但不包括A,B两点
点P在A,B两点之间,但不包括A,B两点![]() 于点M,
于点M,![]() 轴交AB于点N,求MN的最大值;
轴交AB于点N,求MN的最大值;
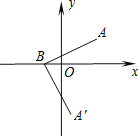
![]() 如图2,将抛物线
如图2,将抛物线![]() 绕顶点旋转
绕顶点旋转![]() 后,再作适当平移得到抛物线
后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第一象限的抛物线
的顶点E在第一象限的抛物线![]() 上,且抛持线
上,且抛持线![]() 与抛物线
与抛物线![]() 交于点D,过点D作
交于点D,过点D作![]() 轴交抛物线
轴交抛物线![]() 于点F,过点E作
于点F,过点E作![]() 轴交抛物线
轴交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点的横坐标为
点的横坐标为![]() 时,四边形DFEG为菱形
时,四边形DFEG为菱形
【解析】
![]() 求直线l与x轴交点A坐标、B坐标,用待定系数法求抛物线
求直线l与x轴交点A坐标、B坐标,用待定系数法求抛物线![]() 的解析式.
的解析式.
![]() 延长PN交x轴于点H,设点P横坐标为m,由
延长PN交x轴于点H,设点P横坐标为m,由![]() 轴可得点N、H横坐标也为m,即能用m表示PN、NH、AH的长.由
轴可得点N、H横坐标也为m,即能用m表示PN、NH、AH的长.由![]() 及对顶角
及对顶角![]() 可得
可得![]() 发现在
发现在![]() 中,MN与PN比值即为
中,MN与PN比值即为![]() ,故先在
,故先在![]() 中求
中求![]() 的值,再代入
的值,再代入![]() ,即得到MN与m的函数关系式,配方即求得MN最大值.
,即得到MN与m的函数关系式,配方即求得MN最大值.
![]() 设点
设点![]() ,所以可设抛物线
,所以可设抛物线![]() 顶点式为
顶点式为![]() 令两抛物线解析式
令两抛物线解析式![]() 列得关于x的方程,解得两抛物线的另一交点D即为抛物线
列得关于x的方程,解得两抛物线的另一交点D即为抛物线![]() 的顶点,故DG
的顶点,故DG![]() ,且求得DF平行且等于GE,即四边形DFEG首先一定是平行四边形.由DFEG为菱形可得
,且求得DF平行且等于GE,即四边形DFEG首先一定是平行四边形.由DFEG为菱形可得![]() ,故此时
,故此时![]() span>为等边三角形.利用特殊三角函数值作为等量关系列方程,即求得e的值.
span>为等边三角形.利用特殊三角函数值作为等量关系列方程,即求得e的值.
解:![]() 直线l:
直线l:![]() 交x轴于点A,
交x轴于点A,
![]() ,解得:
,解得:![]() ,
,
![]() ,
,
![]() 点
点![]() 在直线l上,
在直线l上,
![]() ,
,
![]() ,
,
![]() 抛物线
抛物线![]() :
:![]() 经过点A、B,
经过点A、B,
![]() ,
,
解得: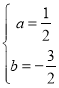 ,
,
![]() 抛物线
抛物线![]() 的解析式为
的解析式为![]() ,
,
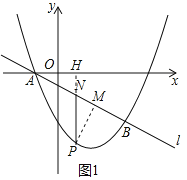
![]() 如图1,延长PN交x轴于点H,
如图1,延长PN交x轴于点H,
![]() ,
,
设![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
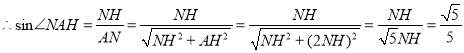 ,
,
![]() 于点M,
于点M,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 的最大值为
的最大值为![]() ,
,
![]() 存在满足条件的抛物线
存在满足条件的抛物线![]() ,使得四边形DFEG为菱形,
,使得四边形DFEG为菱形,
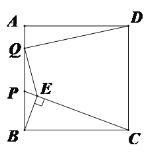
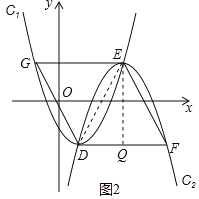
如图2,连接DE,过点E作![]() 于点Q,
于点Q,
![]() ,
,
![]() 抛物线
抛物线![]() 顶点为
顶点为![]() ,
,
设![]() ,
,
![]() 抛物线
抛物线![]() 顶点式为
顶点式为![]() ,
,
当![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 两抛物线另一交点
两抛物线另一交点![]() 为抛物线
为抛物线![]() 顶点,
顶点,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() 四边形DFEG是平行四边形,
四边形DFEG是平行四边形,
若DFEG为菱形,则![]() ,
,
![]() 由抛物线对称性可得:
由抛物线对称性可得:![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
解得:![]() 舍去
舍去![]() ,
,![]() ,
,
![]() 点的横坐标为
点的横坐标为![]() 时,四边形DFEG为菱形.
时,四边形DFEG为菱形.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案