题目内容
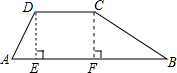
如图,在梯形ABCD中,AB∥CD,∠A=60°,∠B=30°,AD=CD=6,则AB的长为______.


分别过D点,C点作DE⊥AB,CF⊥AB,垂足分别为E,F.
∵∠A=60°,DE⊥AB,
∴∠ADE=30°,
∴AE=
AD=
×6=3.
∴DE=
=
=3
∵AB∥CD,
∴CDEF是矩形,
∴CD=EF,DE=CF=3
,
∵∠B=30°,CF⊥AB,
∴BC=6
,
FB=
=
=9,
∴AB=AE+EF+FB=3+6+9=18.
∵∠A=60°,DE⊥AB,
∴∠ADE=30°,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=
| AD2-AE2 |
| 36-9 |
| 3 |
∵AB∥CD,
∴CDEF是矩形,
∴CD=EF,DE=CF=3
| 3 |
∵∠B=30°,CF⊥AB,
∴BC=6
| 3 |
FB=
| BC2-CF2 |
| 108-27 |
∴AB=AE+EF+FB=3+6+9=18.


练习册系列答案
相关题目